In figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
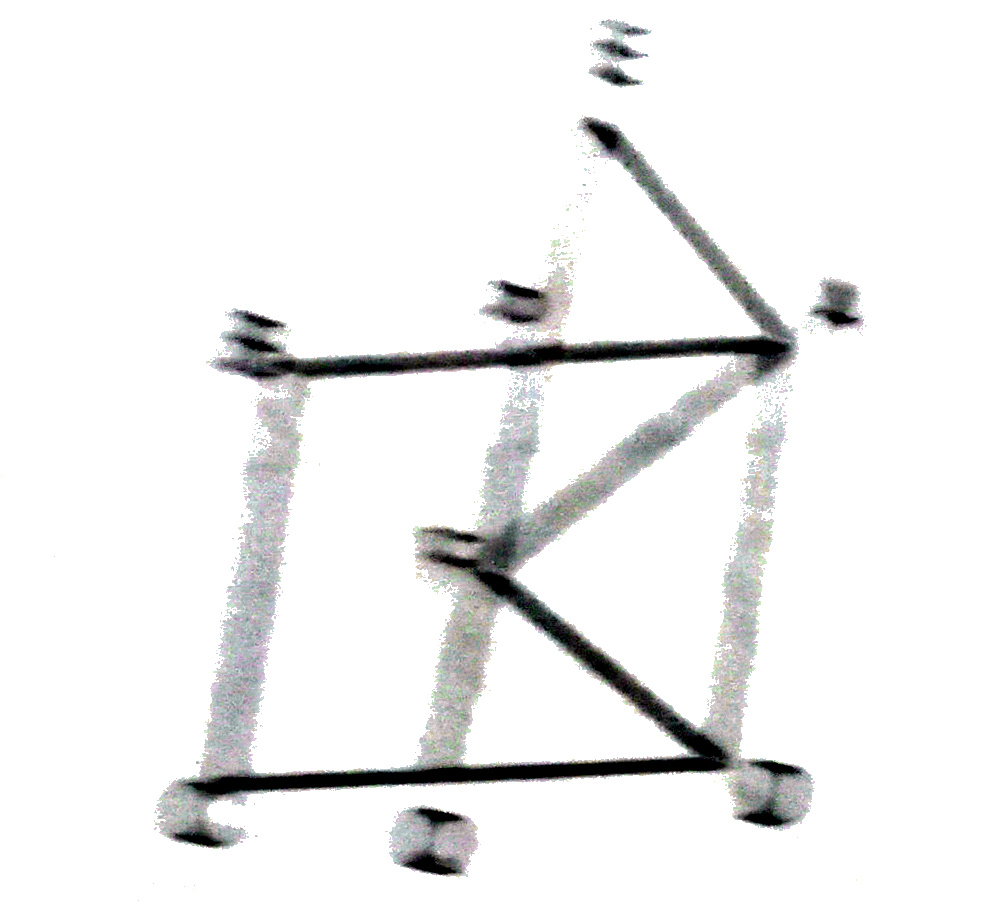
Given: ABCD and AEFD are two parallelograms.
To prove : ar(ΔPEA)=ar(ΔQFD)
Consturction : Join PD.
Proof: In ΔPEAandΔQFD,
∵⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩∠APE=∠DQF(∵ corresponding angles are equal as AB∣∣CD)∠AEP=∠DFQ(∵corresponding angles are equal as AE∣∣DF) AE=DF(∵ opposite sides of a parallelogram are equal)
∴ΔPEA≅ΔQFD (by AAS congruence rule)
Hence, ar(ΔPEA)=ar(ΔQFD) ( ∵ congruent triangles have equal aras)
Topper's Solved these Questions
- AREA OF PARALLELOGRAMS AND TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA OF PARALLELOGRAMS AND TRIANGLESExercise:Exercise
Explore 34 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA OF PARALLELOGRAMS AND TRIANGLESExercise:Revision Exercise (very Short Answer Questions)
Explore 10 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA OF PARALLELOGRAMS AND TRIANGLESExercise:Revision Exercise (long Answer Question)
Explore 5 Videos
- CIRCLE Book:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLE Exercise:Revision Exercise (long Answer Questions )
Explore 5 Videos
Similar Questions
In the adjoining figure, ABCD and PBCQ are parallelogram. Prove that:

ΔABP≅ΔDCQ
View SolutionIn the adjoining figure, ABCD and PBCQ are parallelogram. Prove that:

AP= DQ
View SolutionIn the adjoning figure, ABCD is a parallelogram. Prove that : area of ΔBPC= area of ΔDPQ

View SolutionIn the given figure ABCD is a parallelogram. Prove that AB = 2BC.

View SolutionIn the figure, the area of parallelogram ABCD is

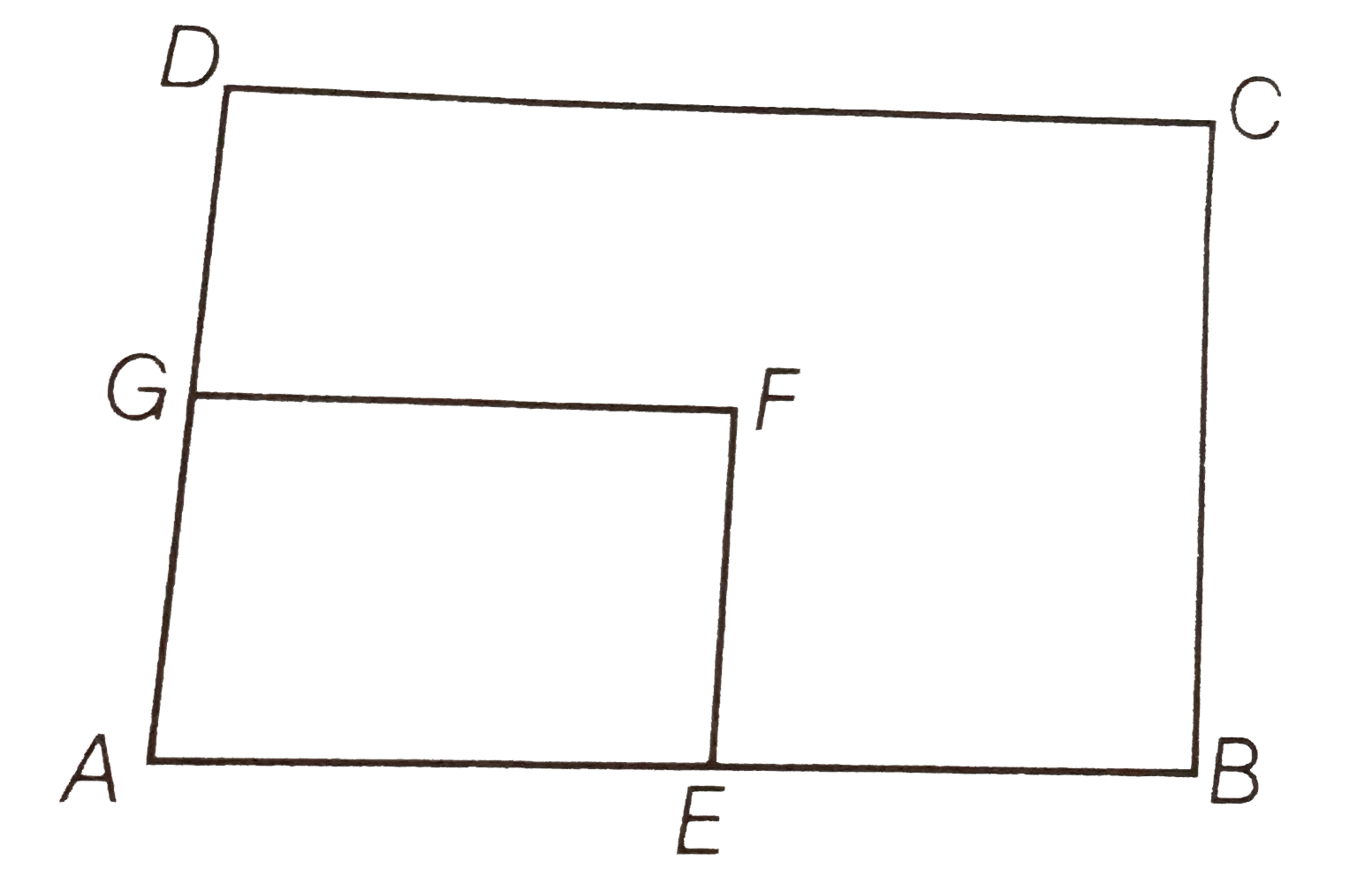
View SolutionIn figure, ABCD and AEFG are two parallelograms. If ∠C=55∘, then determine ∠F.
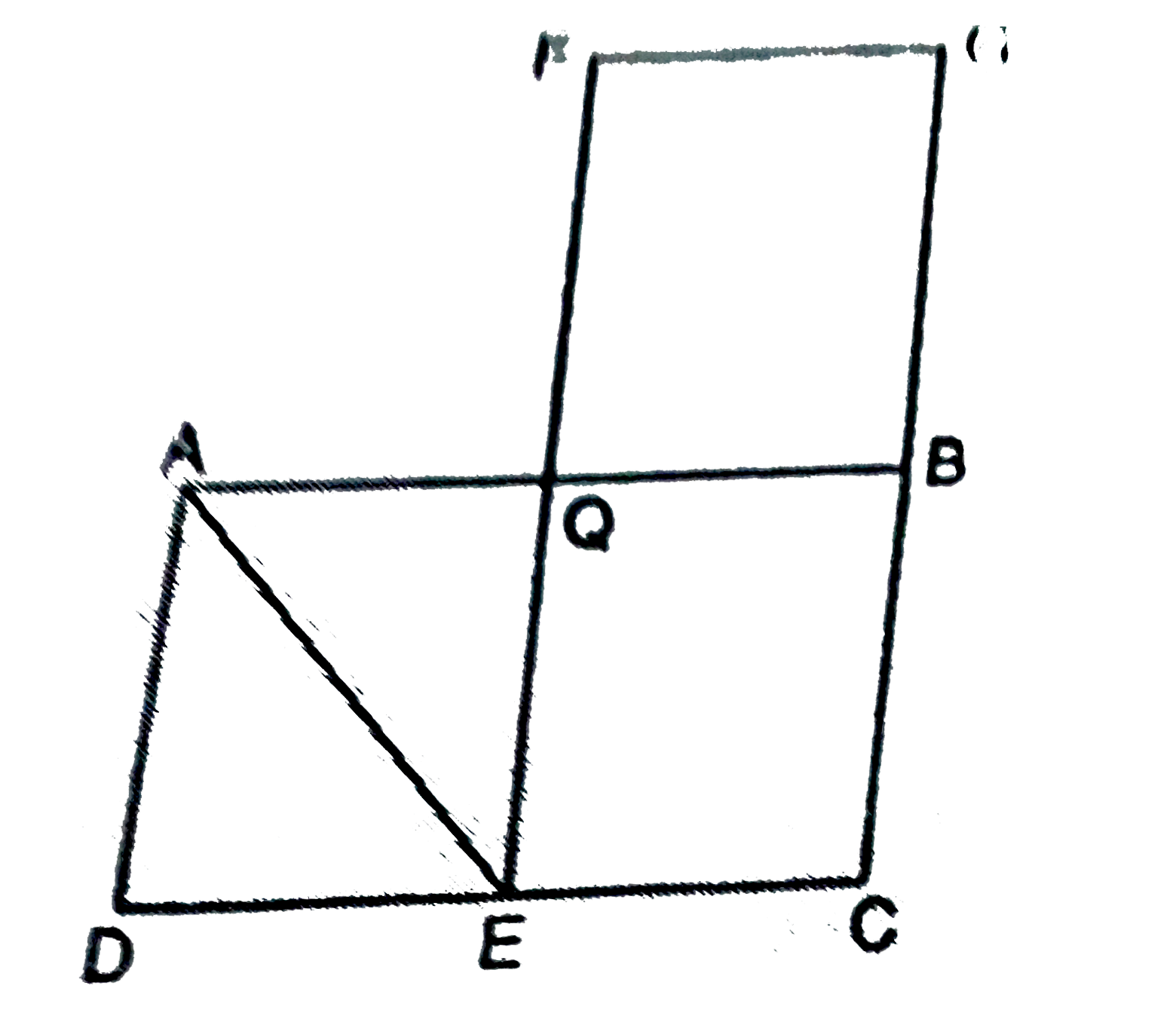
View SolutionIn the given figure, ABCD and FECG are parallelograms equal in area. If ar(ΔAQE)=12cm2, find ar(∣∣gmFGBQ)
View SolutionO is any point on the diagonal PR of a parallelogram PQRS (figure). Prove that ar(ΔPSO)=ar(ΔPQO).

View SolutionIn the given figure, ABCD is a parallelogram. Find the area of ΔAED

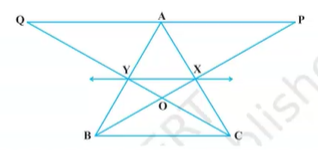
View SolutionIn figure X and Y are the mid-points of AC and AB respectively, QP∣∣BC and CYQ and BXP are straight lines. Prove that ar(ΔABP)=ar(ΔACQ).
View Solution

