In figure X and Y are the mid-points of AC and AB respectively, QP∣∣BC and CYQ and BXP are straight lines. Prove that ar(ΔABP)=ar(ΔACQ).
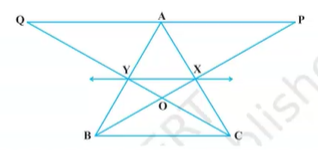
Given X and Y are the mid-points of AC and AB respectively. Also, QP∣∣BC and CYQ, BXP are straight lines.
To prove ar(ΔABP)=ar(ΔACQ)
Proof Since, X and Y are the mid-points of AC and AB respectively.
So, XY∣∣BC
We know that, triangles on the same base and between the same parallels are equal in area.
Here, ΔBYC and ΔBXC lie on same base BC and between the same parallels BC and XY.
So, ar(ΔBYC)=ar(ΔBXC)
On substracting ar(ΔBOC) from both sides, we get
ar(ΔBYC)−ar(ΔBOC)=ar(ΔBXC)−ar(ΔBOC)
⇒ ar(ΔBOY)=ar(ΔCOX)
On adding ar(ΔXOY) both sides, we get
ar(ΔBOY)+ar(ΔXOY)=ar(ΔCOX)+ar(ΔXOY)
⇒ ar(ΔBYX)=ar(ΔCXY) ...(i)
Hence, we observe that quadrilaterals XYAP and YXAQ are on the same base XY and between the same parallels XY and PQ.
∴ ar(XYAP)=ar(YXAQ) ...(ii)
On adding Eqs. (i) and (ii), we get
ar(ΔBYX)+ar(XYAP)=ar(ΔCXY)+ar(YXAQ)
⇒ ar(ΔABP)=ar(ΔACQ) Hence proved.
Topper's Solved these Questions
Similar Questions
In ΔABC , if L and M are the points on AB and AC, respectively such that LM∣∣BC. Prove that ar(ΔLOB)=ar(ΔMOC).
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
BDEF is a parallelogram.
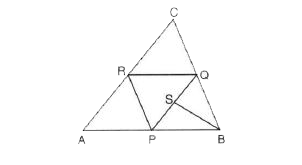
View SolutionThe following figure shows a triangle ABC in which P, Q and R are mid-points of sides AB, BC and CA respectively. S is mid-point of PO.
Prove that : ar.(ΔABC)=8×ar.(ΔQSB)
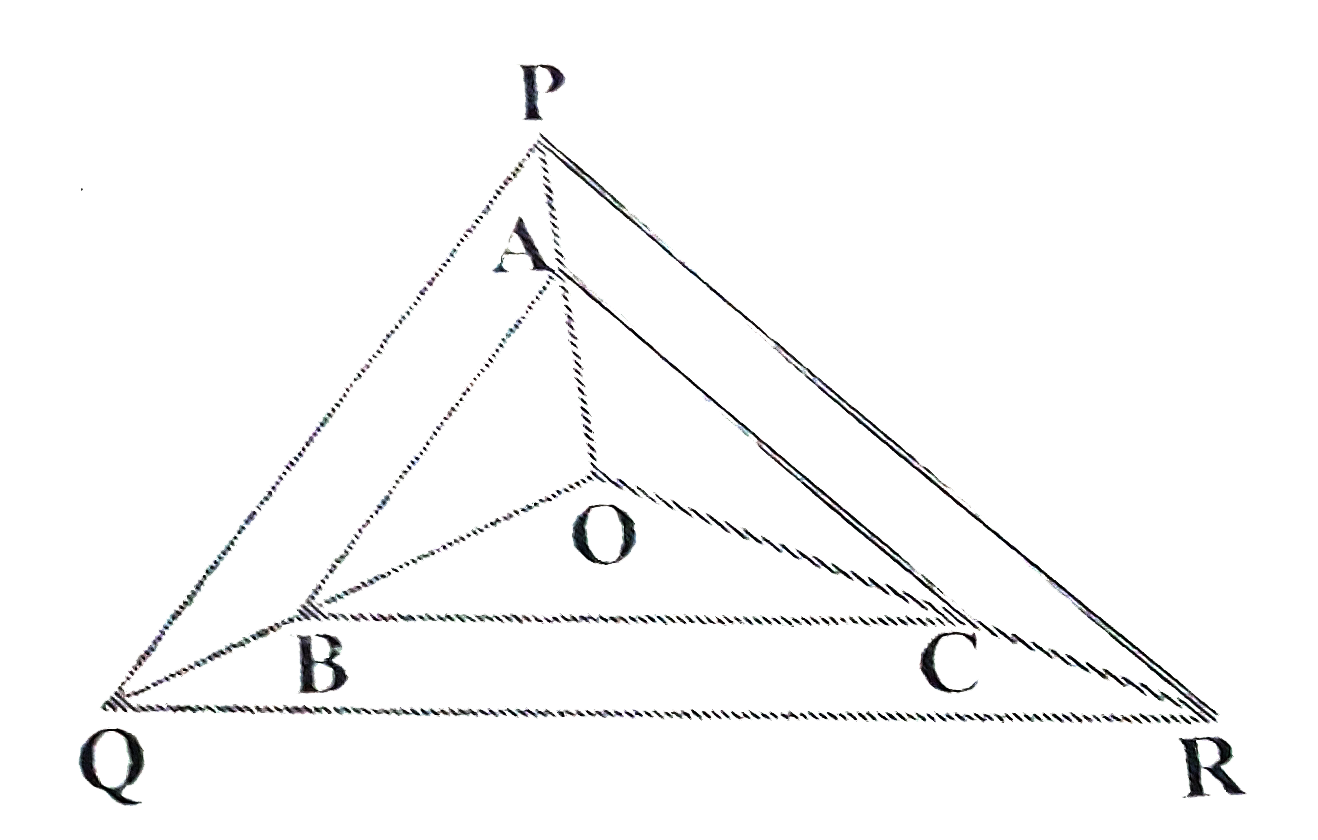
View SolutionIn figure A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
View SolutionIn Δ ABC, D is the mid-point of AB and P is any point on BC. If CQ∣∣PD meets AB and Q (shown in figure), then prove that
ar(ΔBPQ)=12ar(ΔABC).

View SolutionGiven a parallelogram ABCD where X and Y are the mid-points of the sides BC and CD respectively . Prove that:
ar (ΔAXY)=38×ar(/gm)ABCD
View SolutionIn ΔABC,D,E and F are mid-point of sides AB ,BC and AC respectively , Prove that AE and DF bisect each other.
View SolutionIn the adjoning figure, D and E are the points on the sides AB and AC respectively of ΔABC and area of ΔBCE= area of ΔBCD.
Prove that DE∣∣BC

View SolutionIf D,E and F are the mid-points of the sides BC,CA and AB respectively of the ΔABC and O be any point, then prove that OA+OB+OC=OD+OE+OF
View SolutionABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF, prove that ar(ΔAER)=ar(ΔAFR).

View Solution

