Find the mean and variance for each of the data : First 10 multiples of 3.
To find the mean and variance of the first 10 multiples of 3, we will follow these steps:
Step 1: Identify the Data
The first 10 multiples of 3 are:
3,6,9,12,15,18,21,24,27,30
Step 2: Calculate the Sum of the Observations
To find the mean, we first need to calculate the sum of these observations:
Sum=3+6+9+12+15+18+21+24+27+30
We can factor out 3:
Sum=3(1+2+3+4+5+6+7+8+9+10)
The sum of the first 10 natural numbers can be calculated using the formula:
Sum of first n natural numbers=n(n+1)2
For n=10:
Sum=10(10+1)2=10×112=55
Thus, the total sum becomes:
Sum=3×55=165
Step 3: Calculate the Mean
The mean is given by:
Mean=Sum of observationsn
Where n is the number of observations (which is 10):
Mean=16510=16.5
Step 4: Calculate the Sum of Squares of the Observations
Next, we need to calculate the sum of the squares of the observations:
Sum of squares=32+62+92+122+152+182+212+242+272+302
Factoring out 32:
Sum of squares=32(12+22+32+42+52+62+72+82+92+102)
The sum of squares of the first n natural numbers can be calculated using the formula:
Sum of squares=n(n+1)(2n+1)6
For n=10:
Sum of squares=10(10+1)(2×10+1)6=10×11×216=385
Thus, the total sum of squares becomes:
Sum of squares=9×385=3465
Step 5: Calculate the Variance
The variance is given by the formula:
Variance=Sum of squaresn−(Sumn)2
Substituting the values we calculated:
Variance=346510−(16510)2
Calculating each term:
Variance=346.5−(16.5)2=346.5−272.25
Thus, the variance is:
Variance=74.25
Final Results
- Mean: 16.5
- Variance: 74.25
The first 10 multiples of 3 are:
3,6,9,12,15,18,21,24,27,30
To find the mean, we first need to calculate the sum of these observations:
Sum=3+6+9+12+15+18+21+24+27+30
We can factor out 3:
Sum=3(1+2+3+4+5+6+7+8+9+10)
The sum of the first 10 natural numbers can be calculated using the formula:
Sum of first n natural numbers=n(n+1)2
For n=10:
Sum=10(10+1)2=10×112=55
Thus, the total sum becomes:
Sum=3×55=165
The mean is given by:
Mean=Sum of observationsn
Where n is the number of observations (which is 10):
Mean=16510=16.5
Next, we need to calculate the sum of the squares of the observations:
Sum of squares=32+62+92+122+152+182+212+242+272+302
Factoring out 32:
Sum of squares=32(12+22+32+42+52+62+72+82+92+102)
The sum of squares of the first n natural numbers can be calculated using the formula:
Sum of squares=n(n+1)(2n+1)6
For n=10:
Sum of squares=10(10+1)(2×10+1)6=10×11×216=385
Thus, the total sum of squares becomes:
Sum of squares=9×385=3465
The variance is given by the formula:
Variance=Sum of squaresn−(Sumn)2
Substituting the values we calculated:
Variance=346510−(16510)2
Calculating each term:
Variance=346.5−(16.5)2=346.5−272.25
Thus, the variance is:
Variance=74.25
- Mean: 16.5
- Variance: 74.25
Topper's Solved these Questions
- STATISTICSBook:NAGEEN PRAKASHAN ENGLISHChapter:STATISTICSExercise:MISCELLANEOUS EXERCISE
Explore 7 Videos
- STATISTICSBook:NAGEEN PRAKASHAN ENGLISHChapter:STATISTICSExercise:EXERCISE
Explore 20 Videos
- SETSBook:NAGEEN PRAKASHAN ENGLISHChapter:SETSExercise:MISC Exercise
Explore 16 Videos
- STRAIGHT LINESBook:NAGEEN PRAKASHAN ENGLISHChapter:STRAIGHT LINESExercise:Exercise
Explore 207 Videos
Similar Questions
Find the mean and variance for each of the data in Question:

View SolutionFind the mean and variance for each of the data in Question:
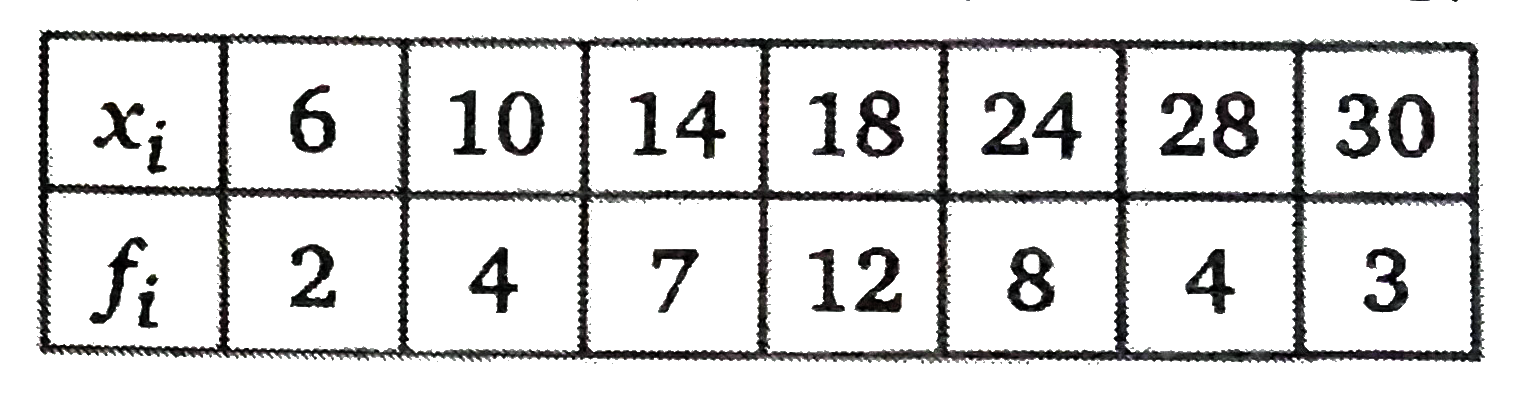
View SolutionFind the mean and variance for each of the data : First n natural numbers
View SolutionFind the mean and variance for each of the data : 6,7,10,12,13,4,8,12
View SolutionFind the sum of first 8 multiples of 3.
View SolutionThe variance of first 10 multiples of 3 is
View SolutionFind the variance of first 10 multiples of 3
View SolutionFind the mean of first five multiples of 3.
View SolutionFind the mean of first five multiples of 3.
View SolutionFind the mean and variance for the following frequency distributions in
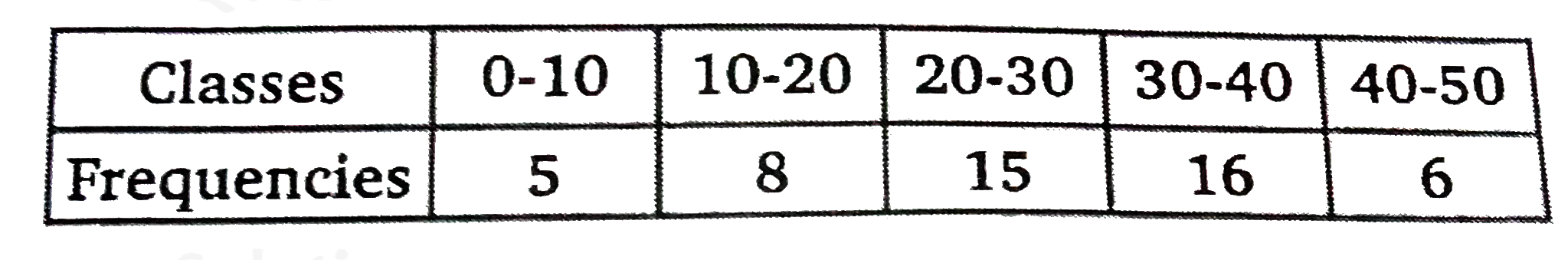
View Solution

