In Question 4, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
Let the given line AB has two mid-points C and D.
∴ AC=CB (∵ C is the mid-point of AB)….(1)
and AD=DB (∵ D is the mid-point of AB)….(2)
Subtracting eq. (2) from eq. (1), we get
AC−AD=CB−DB
⇒ −(AD−AC)=CB−DB
⇒ −CD=CD
or CD−CD=CD+CD (if equals added to equals then wholes are equal)
⇒ 0=2CD
⇒ CD=0
∴ C and D coincide.
Thus, every line segment has one and only mid-point. Hence Proved.
Topper's Solved these Questions
- INTRODUCTION TO EUCLID'S GEOMETRYBook:NAGEEN PRAKASHAN ENGLISHChapter:INTRODUCTION TO EUCLID'S GEOMETRYExercise:Exercise
Explore 8 Videos
- INTRODUCTION TO EUCLID'S GEOMETRYBook:NAGEEN PRAKASHAN ENGLISHChapter:INTRODUCTION TO EUCLID'S GEOMETRYExercise:Exercise
Explore 8 Videos
- HERONS'S FORMULABook:NAGEEN PRAKASHAN ENGLISHChapter:HERONS'S FORMULAExercise:Revision Exercise
Explore 11 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBook:NAGEEN PRAKASHAN ENGLISHChapter:LINEAR EQUATIONS IN TWO VARIABLESExercise:Revision Exercise
Explore 12 Videos
Similar Questions
Knowledge Check
A line segment has _________ end points.
A0B1C2D4
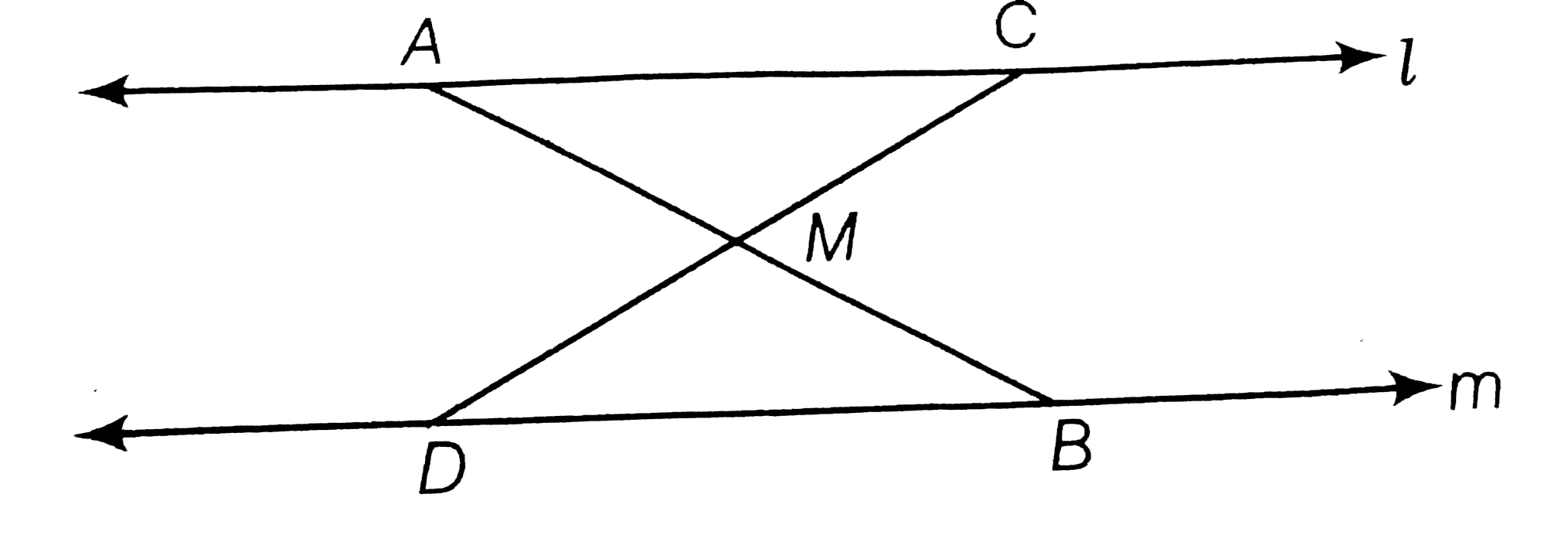
In Figure, l∣∣m and M is the mid-point of the line segment AB . Prove that M is also the mid-pooint of any line segment CD having its end-points on l and m respectively.
View SolutionIn the given figure l||m and M is the mid-point of a line segment AB .Show that M is also the mid- point of any line segment CD, having its end points on l and m, respectively.
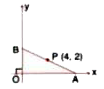
View SolutionIn the given figure, P (4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
View SolutionThe mid point of the line segment joining the points (−5,7)and(−1,3) is
View SolutionFind the mid-point of the line segment joining the points :
(5, -3) and (-1, 7)
View SolutionFind the mid-point of the line segment joining the points :
(-6, 7) and (3, 5)
View SolutionPoints AandB lie on the parabola y=2x2+4x−2, such that origin is the mid-point of the linesegment AB. If l be the length of the line segment AB, then find the unit digit of l2.
View Solution

