ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD=/_CBD.Solution in Punjabi
Step by step video & image solution for ABC and ADC are two right triangles with common hypotenuse AC. Prove that /_CAD = /_CBD. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Given an arc of a circle, complete the circle.
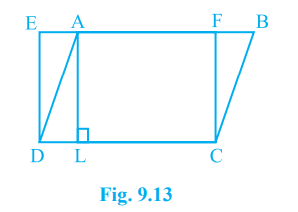
View SolutionIn Fig. 9.13, ABCD is a parallelogram and EFCD is a rectangle. Also, AL⊥DC. Prove that (i) ar (ABCD) = ar (EFCD) (ii) ar (ABCD) = DC × AL
View SolutionConstruct a triangle ABC, in which ∠B=60∘, ∠C=45∘ and AB + BC + CA = 11 cm.
View SolutionABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD =∠CBD.
View SolutionShow that in a right triangle the hypotenuse is the longest side. GIVEN : A right triangle ABC in which ∠ABC=900. TO PROVE : Hypotenuse AC is the longest side, i.e. AC>AB (ii) AC>BC
View SolutionABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD=∠CBD.
View Solution△ABC AND △ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD=∠CBD.
View SolutionIf D is the mid-point of the hypotenuse AC of a right triangle ABC, prove that BD=12AC
View SolutionIn the adjoining figure, AB=AC and BD=DC Prove that Delta ADB-=Delta ADC and hence show that (i) /_ADB-=/_ADC=90^(@) , (ii) /_BAD=/_CAD
View Solutionउभयनिष्ट कर्ण AC वाले दो समकोण त्रिभुज ABC और ADC है । सिद्ध कीजिए कि ∠CAD=∠CBD है।
View Solutionउभयनिष्ठ कर्ण AC वाले दो समकोण त्रिभुज ABC और ADC है, सिध्द कीजिए कि ∠CAD=∠CBD है।
View SolutionAC is the common hypotneus of the right-angled triangels ABC and ADC. Prove that ∠CAD=∠CBD
View Solutionयदि D समकोण त्रिभुज ABC के कर्ण AC का मध्य-बिन्दु हों,तो सिध्द करो कि
BD=12AC
View SolutionABC and ADC are two right triangle with common hypotenuse AC. Prove that CAD = CBD.

View Solutiontriangle ABC and triangle ADCs are two right-angled triangles with common diagonal AC /_ CAD = /_CBD Prove that.
View Solution/_ABC And /_ADC Are two right triangles with common diagonal AC /_CAD= /_CBD Prove that.
View Solution
