D, E and F are respectively the mid-points of the sides BC, CA and AB of a △ABC. Show that:- BDEF is a parallelogram.Solution in Punjabi
Step by step video & image solution for D, E and F are respectively the mid-points of the sides BC, CA and AB of a triangle ABC. Show that:- BDEF is a parallelogram. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
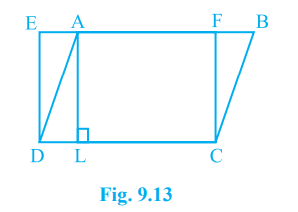
In Fig. 9.13, ABCD is a parallelogram and EFCD is a rectangle. Also, AL⊥DC. Prove that (i) ar (ABCD) = ar (EFCD) (ii) ar (ABCD) = DC × AL
View SolutionGiven an arc of a circle, complete the circle.
View SolutionD, E, F are the mid points of side AB, BC, AC prove that BDEF is a parallelogram whose area is half that of Δ ABC
View SolutionD,E and F are respectively the mid-points of the sides BC,CA and AB of a /_ABC. Show that (i) BDEF is a parallelogram
View SolutionD, E and F are the mid-points of the sides BC, CA and AB, respectively of and equilateral ΔABC. Show that ΔDEF is also an equilateral triangle.
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB respectively of ΔABC. Prove that:
(i) □BDEF is a parallelogram
(ii) area of ΔDEF=14× area of ΔABC
(iii) area of □BDEF=12× area of ΔABC

View SolutionD,E and F are respectively the mid-points of the sides BC, CA and AB of △ABC show that
(i) BDEF is a parallelogram.
(ii) ar (DEF) = 14 ar (ABC)
(iii) ar(BDEF)=12 ar (ABC)
View SolutionABC is a triangle and D,E,F are the mid-points of the sides BC,CA, AB respectively . The ratio of the areas of ΔABCandΔDEF is :
View SolutionD, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral ΔABC. Show that ΔDEF is also an equilateral triangle.
View SolutionD, E, F are the mid points of side AB, BC, AC prove that BDEF is a parallelogram whose area is half that of Δ ABC
View SolutionD, E ਅਤੇ F ਕ੍ਰਮਵਾਰ ਤ੍ਰਿਭੁਜ ABC ਦੀਆਂ ਭੁਜਾਵਾਂ BC,CA ਅਤੇ AB ਦੇ ਮੱਧ-ਬਿੰਦੂ ਹਨ।ਦਰਸਾਉ ਕਿ:- BDEF ਇੱਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ।
View SolutionIf D,E,F are the mid-point of sides AB,BC and CA respectively of △then the ratio of the areas of triangles △DEF and ABC is
View SolutionIn ΔABC,AB=AC.D,Eand F are mid-points of the sides BC, CA and AB respectively . Show that :
AD is perpendicular to EF.
View SolutionIn ΔABC,AB=AC.D,Eand F are mid-points of the sides BC, CA and AB respectively . Show that :
AD and FE bisect each other.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
BDEF is a parallelogram.
View Solution

