An horizontal insulated cylindrical vessel of length 2l is separated by a thin insulating piston into two equal parts as shown. Each part contains n moles of an ideal monoatomic gas at temperature T. The piston is connected to end faces of cylinder with help of two springs each of spring constank k. Initially both springs are in relaxed state. The temperature of left part of cylinder is kept constant by some external means while heat is supplied to right part with help of filament. Answer following questions.
heat given by left part of cylinder to external arrangement is
To solve the problem, we will break it down into steps:
Step 1: Understand the System
We have a horizontal insulated cylindrical vessel divided into two equal parts by a piston. Each part contains n moles of an ideal monoatomic gas at temperature T. The left part is isothermal (constant temperature), while heat Q is supplied to the right part.
Step 2: Initial Conditions
Initially, both parts of the cylinder have the same volume V=A⋅L (where A is the cross-sectional area and L is the length of each part). The pressure in both parts is given by the ideal gas equation:
P0=nRTV=nRTAL
Step 3: Changes Due to Heat Addition
When heat Q is supplied to the right part, the piston moves to the left by L4. This results in:
- The volume of the left part becomes V1=A⋅(L−L4)=3AL4
- The volume of the right part becomes V2=A⋅(L+L4)=5AL4
Step 4: Calculate the Pressure in Each Part
Using the ideal gas law for the left part (isothermal):
P1=nRTV1=nRT3AL4=4nRT3AL=43P0
For the right part:
Let P2 be the pressure in the right part. The equilibrium condition gives:
P1A+kL4+kL4=P2A
This simplifies to:
P2=P1+kL2A
Substituting P1:
P2=43P0+kL2A
Step 5: Change in Internal Energy of the Right Part
The change in internal energy ΔU for the right part can be calculated as:
ΔU=nCvΔT
For a monoatomic gas, Cv=32R. We need to find ΔT.
Step 6: Final Temperature Calculation
Using the ideal gas law for the right part:
T2=P2V2nR
Substituting P2 and V2:
T2=(43P0+kL2A)⋅5AL4nR
This gives us the final temperature T2.
Step 7: Heat Given by the Left Part
The heat given by the left part can be calculated using the first law of thermodynamics:
Q=ΔU+W
Where W is the work done by the gas. The work done can be expressed in terms of the potential energy stored in the springs:
W=kL216
Thus, the heat given by the left part is:
Q−ΔU=W
Final Expression for Heat Given by Left Part
Putting it all together, we find that:
Q−(ΔU)=Q−(1516kL2+nRT)=kL216
Conclusion
The heat given by the left part of the cylinder to the external arrangement is:
Q−(1516kL2+nRT)
We have a horizontal insulated cylindrical vessel divided into two equal parts by a piston. Each part contains n moles of an ideal monoatomic gas at temperature T. The left part is isothermal (constant temperature), while heat Q is supplied to the right part.
Initially, both parts of the cylinder have the same volume V=A⋅L (where A is the cross-sectional area and L is the length of each part). The pressure in both parts is given by the ideal gas equation:
P0=nRTV=nRTAL
When heat Q is supplied to the right part, the piston moves to the left by L4. This results in:
- The volume of the left part becomes V1=A⋅(L−L4)=3AL4
- The volume of the right part becomes V2=A⋅(L+L4)=5AL4
Using the ideal gas law for the left part (isothermal):
P1=nRTV1=nRT3AL4=4nRT3AL=43P0
Let P2 be the pressure in the right part. The equilibrium condition gives:
P1A+kL4+kL4=P2A
This simplifies to:
P2=P1+kL2A
Substituting P1:
P2=43P0+kL2A
The change in internal energy ΔU for the right part can be calculated as:
ΔU=nCvΔT
For a monoatomic gas, Cv=32R. We need to find ΔT.
Using the ideal gas law for the right part:
T2=P2V2nR
Substituting P2 and V2:
T2=(43P0+kL2A)⋅5AL4nR
This gives us the final temperature T2.
The heat given by the left part can be calculated using the first law of thermodynamics:
Q=ΔU+W
Where W is the work done by the gas. The work done can be expressed in terms of the potential energy stored in the springs:
W=kL216
Thus, the heat given by the left part is:
Q−ΔU=W
Putting it all together, we find that:
Q−(ΔU)=Q−(1516kL2+nRT)=kL216
The heat given by the left part of the cylinder to the external arrangement is:
Q−(1516kL2+nRT)
Similar Questions
An horizontal insulated cylindrical vessel of length 2l is separated by a thin insulating piston into two equal parts as shown. Each part contains n moles of an ideal monoatomic gas at temperature T. The piston is connected to end faces of cylinder with help of two springs each of spring constank k. Initially both springs are in relaxed state. The temperature of left part of cylinder is kept constant by some external means while heat is supplied to right part with help of filament. Answer following questions.
temperature of gas in right part in final equilibrium is
View SolutionAn horizontal insulated cylindrical vessel of length 2l is separated by a thin insulating piston into two equal parts as shown. Each part contains n moles of an ideal monoatomic gas at temperature T. The piston is connected to end faces of cylinder with help of two springs each of spring constank k. Initially both springs are in relaxed state. The temperature of left part of cylinder is kept constant by some external means while heat is supplied to right part with help of filament. Answer following questions.
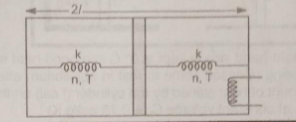
If energy Q is supplied to right part so that the piston moves to left by l/4 then change in internal energy of right part of cylinder is
View Solution
Knowledge Check
A spring of spring constant k is cut in three equal pieces. The spring constant of each part will be
Ak3B3kCkDk6A cylindrical vessel made of thermally insulating material is divided into two equal parts by an insulating and. Movable piston. Both parts contain ideal monoatomic gas . The gas in the left part is supplied heat such that the volume of right part becomes one-eight of its initial volume . Work done by the gas in the right part is
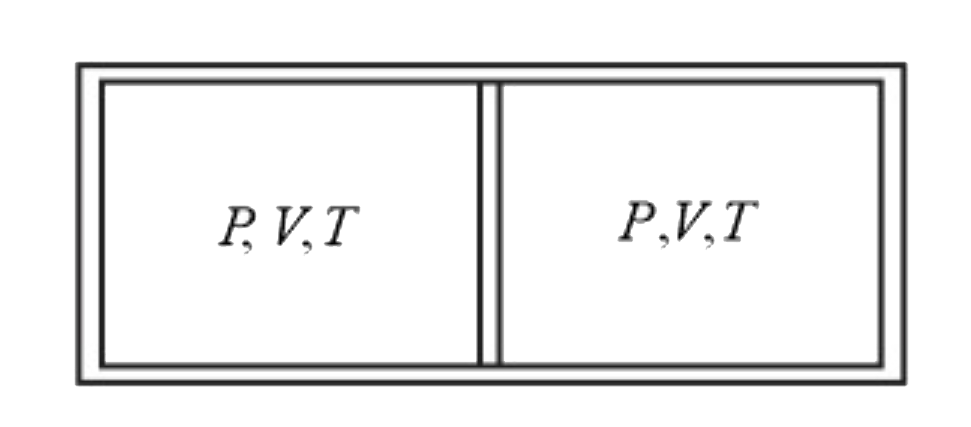 A−92PVB92PVC−3PVD3PV
A−92PVB92PVC−3PVD3PVA spring of force constant k is cut into there equal part what is force constant of each part ?
AK3B3KCKD2K
A thermally insulated vessel is divided in to two parts by a heat insulating piston which can move in the vessel without the friction. The left part of the vessel contains one mole of an ideal monatomic gas, & the right part is empty. The piston is connected to the right wall of the vessel through a spring whose length in free state is equal to the length of the vessel as shown in the figure. Determine the heat capacity C of the system, neglecting the heat capacity of the vessel, piston and spring.

View SolutionA spring having a spring constant k is divded into three parts. Calculate the force constant for each part.
View SolutionA spring of force constant k and natural length 6l is broken in three parts of length ratio 1:2:3 find the spring constant of each part.
View SolutionA horizontally kept cylindrical vessel closed at both ends is separated into two equal (42 cm each) parts by an adiabatic piston. Both parts contain gas having equal mass at a temperature of 27∘C and a pressure of 1 atm. How much should the gas be heated in one part of the cylinder to shift the piston by 2 cm? Find the pressure p of the gas after shifting of the piston.
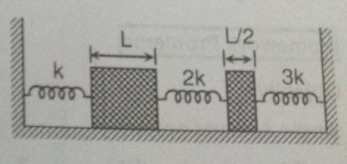
View SolutionThe system shown in figure consists of three springs and two rods as shown. If the temperature of the rods is increased by δ(t) calculate the energy stored in each of the springs. The springs are initially relaxed. There is no friction.
View Solution

