If the chord of contact of tangents from a point P to the parabola y2=4ax touches the parabola x2=4by, then find the locus of P.
A circle
A parbola
A pair of straight lines
A hyperbola
The correct Answer is:D
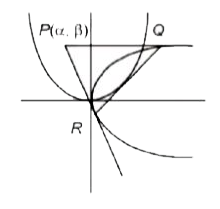
QR:yβ=2a(x+α)
y=2aβ(x+α)
Parabola : x2=4by
⇒y=2aβ(x+α)
Parabola: x2=4by
⇒x2=4b.2aβ⇒βx2=8ab(x+α)⇒Bx2−8ax−8abα=0 ∵ D=0
⇒64a2b2+32abαβ=0⇒αβ=642b232ab=−2ab⇒Locus of (α,β) is a hyperbola
Similar Questions
The equation of the chord of contact of tangents from (2, 5) to the parabola y2=8x, is
View SolutionThe equation of the chord of contact of tangents from (2, 5) to the parabola y2=8x, is
View SolutionA point P moves such that the chord of contact of the pair of tangents from P on the parabola y2=4ax touches the rectangular hyperbola x2−y2=c2. Show that the locus of P is the ellipse x2c2+y2(2a)2=1.
View SolutionIf the chord of contact of tangents from a point P(h, k) to the circle x2+y2=a2 touches the circle x2+(y−a)2=a2, then locus of P is
View SolutionIf the chord of contact of tangents from a point (x1,y1) to the circle x2+y2=a2 touches the circle (x−a)2+y2=a2, then the locus of (x1,y1) is
View SolutionFind the points of contact Q and R of a tangent from the point P(2,3) on the parabola y2=4x.
View SolutionFind the points of contact Q and R of a tangent from the point P(2,3) on the parabola y2=4x.
View SolutionThe points of contact of the tangents drawn from the point (4, 6) to the parabola y2=8x
View SolutionIf the tangent at the point P(2,4) to the parabola y2=8x meets the parabola y2=8x+5 at QandR, then find the midpoint of chord QR.
View SolutionIf the tangent at the point P(2,4) to the parabola y2=8x meets the parabola y2=8x+5 at QandR, then find the midpoint of chord QR.
View Solution
