The curve is given by x=cos2t,y=sint represents
A
A parabola
B
Circle
C
Part of a parabola
D
A pair of straight lines
Video Solution
Text Solution
The correct Answer is:C
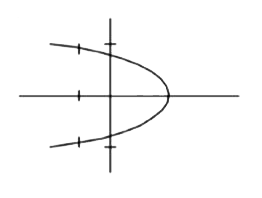
Given parabola equations are
x=cos2t,y=sint
⇒ Obviously, x,y∈[−1,1]
∴x=1−2sin2t=1−2y2
⇒2y2=1−x=−(x−1)
⇒y2=−12(x−1)
⇒ It represents a part of a parabola
|
Similar Questions
Knowledge Check
The tangent to the curve given by x=etcosty=et sint at t =π4 makes with x-axis an angle of
A0Bπ4Cπ3Dπ2
x=sint,y=cos2t
View SolutionThe transverse displamcement y(x,t) of a wave y(x,t ) on a string is given by yox, t) = . This represents a
View Solutionx=2cos2t,y=6sin2t find dydx
View SolutionFind the equation of tangent to the curve given by x=2sin3t,y=2cos3t at a point where t=π2 ?
View SolutionA curve is represented parametrically by the equations x=etcostandy=etsint where t is a parameter. Then The relation between the parameter 't' and the angle a between the tangent to the given curve andthe x-axis is given by, 't' equals
View SolutionThe equation of the tangent to the curve x=tcost,y=tsint at the origin, is
View SolutionThe curve represented by x=2(cost+sint)andy=5(cost−sint) is
View Solution
