A uniform rod of length 1.00 m is suspended through an end and is set into oscillation with small amplitude under gravity. Find the time period of oscillation.
1.60 s
1.80 s
2.00 s
2.40 s
The correct Answer is:D
T=2π√I0+mh2mgh
where I0=ml2/12
h=l2
So, T=2.40s
Similar Questions
A uniform rod of length 2.0 m is suspended through an end and is set into oscillation with small amplitude under gravity. The time period of oscillation is approximately
View SolutionA uniform rod of length 2.0 m is suspended through its endpoint about which it performs small angular oscillations in the vertical plane, its time period is nearly
View SolutionAn infinite nonconducting sheet has surface charge density s. There is a small hole in the sheet as shown in the figure. A uniform rod of length l having linear charge density λ is hinged in the hole as shown. If the mass of the rod is m, then the time period of oscillation for small angular displacement is
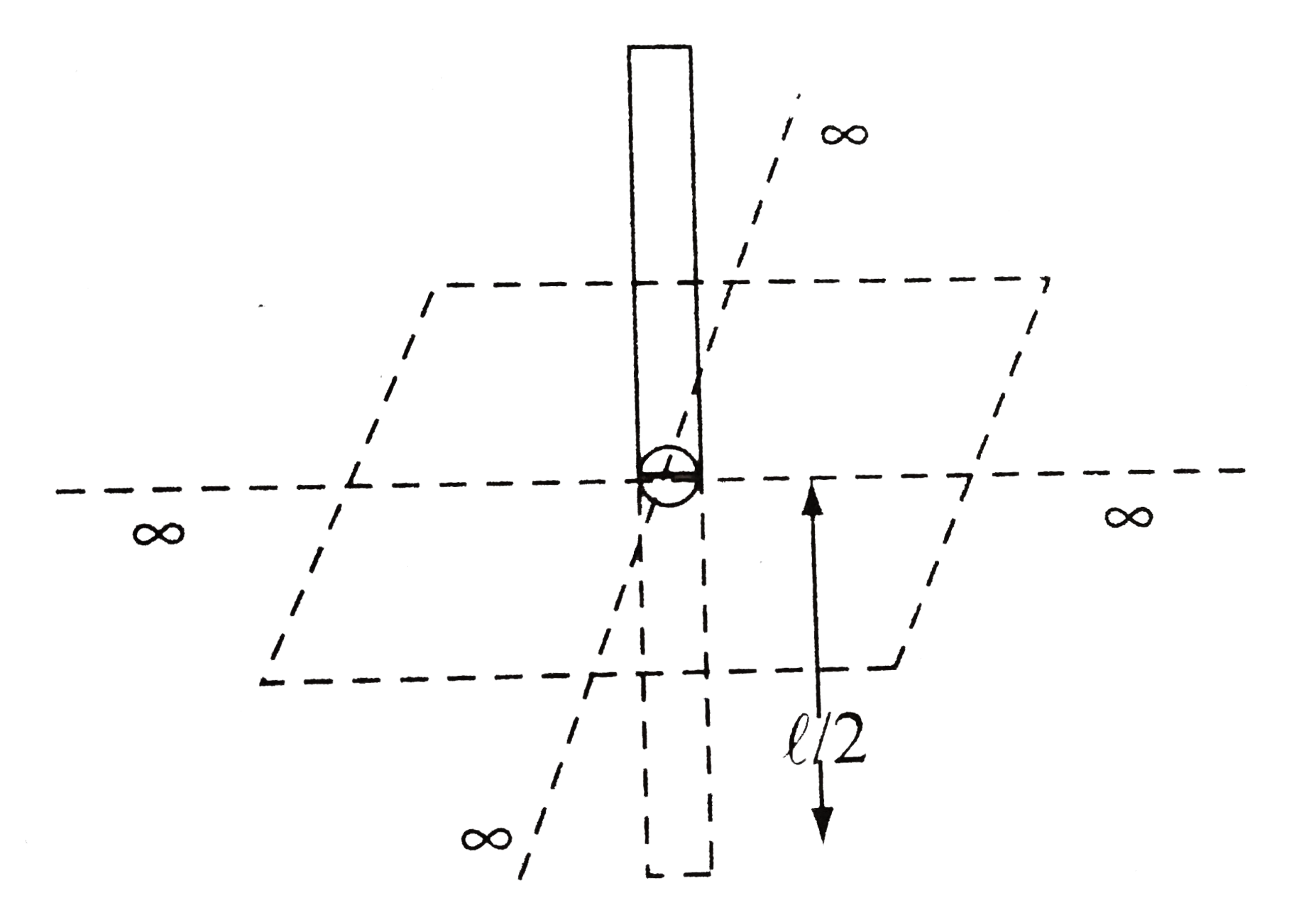View SolutionA uniform rod of mass m and length l is suspended through a light wire of length l and torsional constant k as shown in figure. Find the time perid iof the system makes a. small oscillations in the vertical plane about the suspension point and b. angular oscillations in the horizontal plane about the centre of the rod.
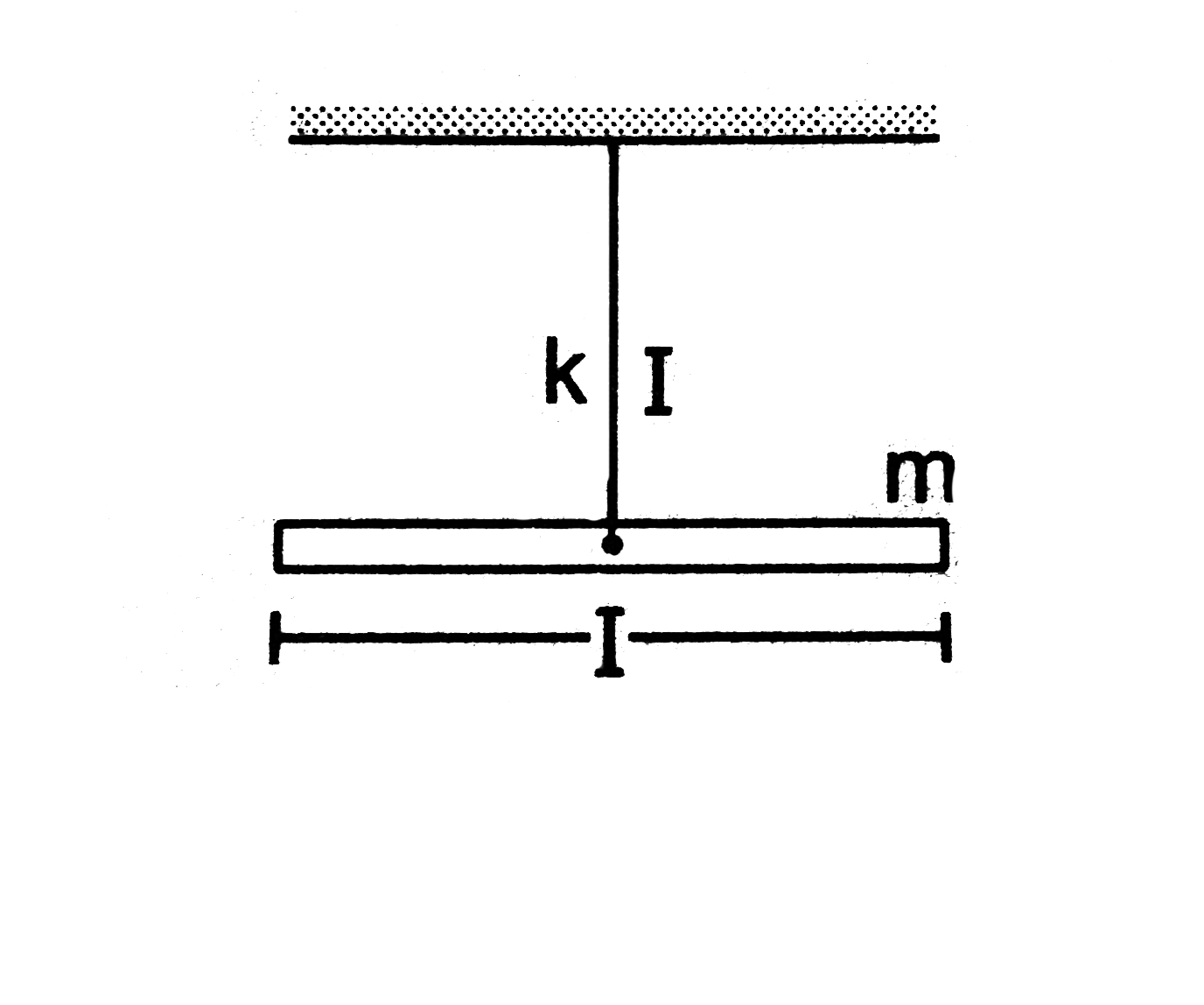View SolutionA uniform rod of length l is suspended from a point P. and the rod is made to undergo small oxcillations. Match the following
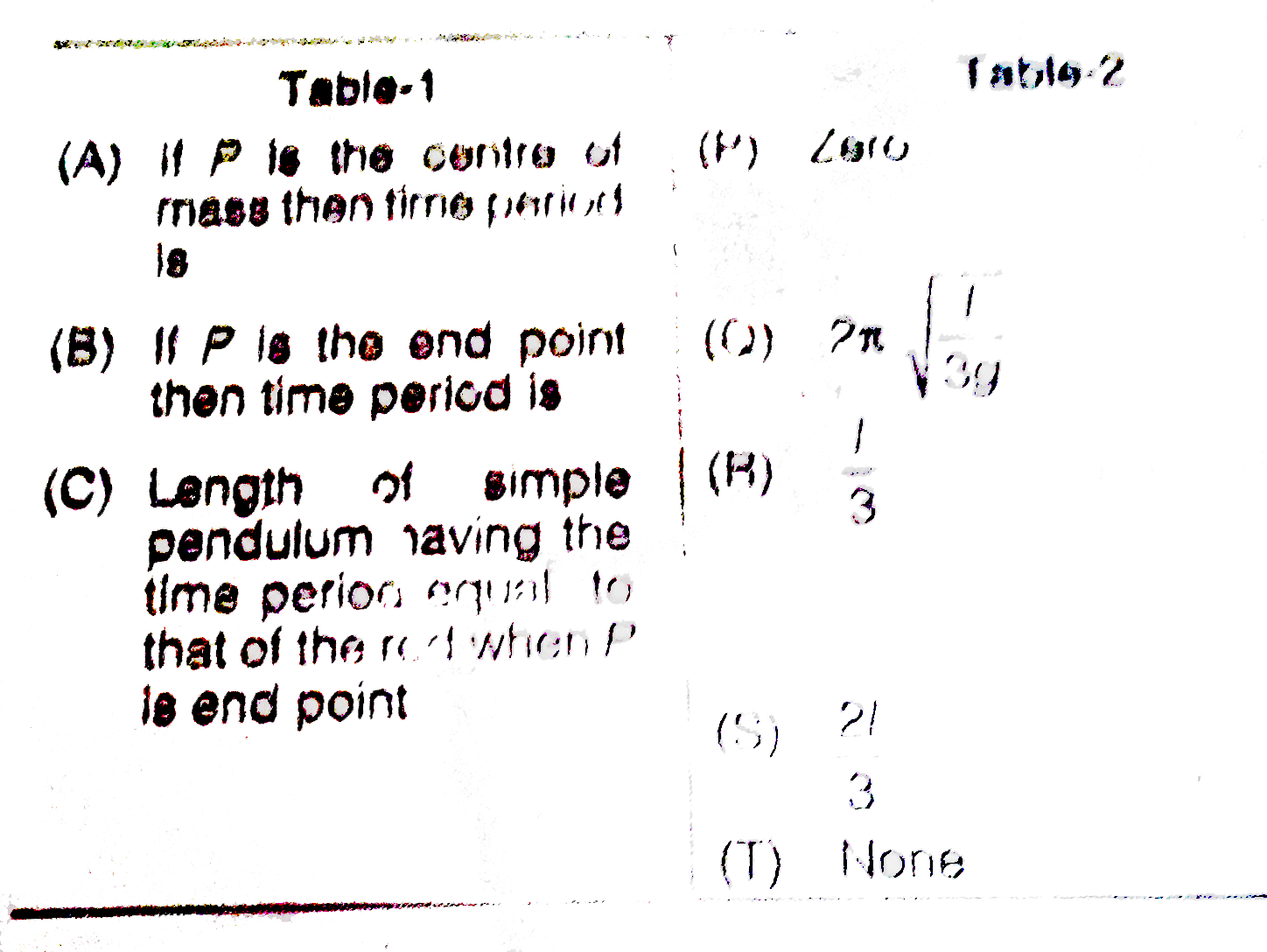View SolutionA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
View SolutionA thin rod of length L is hanging from one end and free to oscillate like s compound pendulum about a horizontal axis, Its time period for small oscillations is
View SolutionA uniform rod of length l is pivoted distance x from the top of the rod . Neglecting friction find the (a) value of x for minimum period of oscillation, (b) minimum period of oscillation of the rod.
View SolutionA uniform rod of length l oscillates about an axis passing through its end. Find the oscillation period and the reduced length of this pendulum.
View SolutionThe time period of small oscillations of mass m :-
_S01_040_Q01.png)
View Solution