The line xa−yb=1 cuts the x-axis at P. The equation of the line through P and perpendicular to the given line is
x+y=ab
x+y=a+b
ax+by=a2
bx+ay=b2
The correct Answer is:C
Line perpendicular to the given line xa−yb=1
xb+ya+λ=0
According to the question, line (i) is passing through the point P(a, 0)
ab+0+λ=0
λ=−ab
Put the value of λ in equation (i), we get xb+ya−ab=0
ax+by=a2
Topper's Solved these Questions
- JEE MAIN - 5Book:VMC MODULES ENGLISHChapter:JEE MAIN - 5Exercise:PART III : MATHEMATICS (SECTION-2)
Explore 5 Videos
- INVERSE TRIGONOMETRYBook:VMC MODULES ENGLISHChapter:INVERSE TRIGONOMETRYExercise:JEE ADVANCED ( ARCHIVE )
Explore 10 Videos
- JEE MAIN REVISION TEST - 30 | JEE -2020Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 30 | JEE -2020Exercise:MATHEMATICS
Explore 25 Videos
Similar Questions
Find the equation of the line through point (−2,−1) and perpendicular to the line y=x.
View SolutionWrite down the equation of the line AB, through (3, 2) and perpendicular to the line 2y=3x+5.
View SolutionFind the equation of the straight line through (2, 3) and perpendicular to the line 4x−3y=10
View Solutionfind the equation of a line passing through (3,-2)and perpendicular to the line x−3y+5=0
View SolutionThe line segment joining the points A (3,-4) and B (-2, 1) is divided in the ratio 1:3 at point P in it. Find the co-ordinates of P.
Also, find the equation of the line through P and perpendicular to the line 5x–3y=4.
View SolutionThe equation of the line passing through the point (1,2) and perpendicular to the line x+y+1=0 is
View SolutionThe equation of the line passing through the point (1,2) and perpendicular to the line x+y+1=0 is
View SolutionA line AB meets X-axis at A and Y-axis at B. P(4, -1) divides AB in the ratio 1:2.
(ii) Find the equation of the line through P and perpendicular to AB
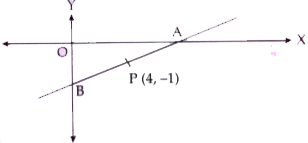
View SolutionFind the equation of a line passes through the point (−2,1) and perpendicular to the line 3x+y=5.
View SolutionFind the equation of a line passing through the point (−1,0) and perpendicular to the line x+5y=4.
View Solution