In a circle with centre 'O' PA and PB are two chords. PC is the chord that bisects the angle . APB The tangent to the circle at C is drawn meeting PA and PB extended at Q and R respectively. If QC = 3, QA = 2 and RC = 4, then length of RB equals
The correct Answer is:11
To solve the problem, we will follow these steps systematically:
Step 1: Understand the Geometry
We have a circle with center 'O', chords PA and PB, and a chord PC that bisects the angle ∠APB. A tangent at point C meets the extensions of PA and PB at points Q and R, respectively. We are given the lengths QC = 3, QA = 2, and RC = 4, and we need to find the length of RB.
Step 2: Use the Power of a Point Theorem
According to the Power of a Point theorem, for point P, we have:
PQ⋅PA=QC2
Let PQ = x. Then:
x⋅2=32
x⋅2=9
x=92
Step 3: Find PR Using Similar Triangles
Using the sine rule in triangle PQR, we can relate the segments:
QCPQ=RCPR
Substituting the known values:
392=4PR
Cross-multiplying gives:
3⋅PR=4⋅92
3⋅PR=18
PR=6
Step 4: Use the Power of a Point Again
Now, we apply the Power of a Point theorem again for triangle PCR:
PR⋅RB=RC2
Substituting the known values:
6⋅RB=42
6⋅RB=16
RB=166=83
Conclusion
Thus, the length of RB is:
83
---
We have a circle with center 'O', chords PA and PB, and a chord PC that bisects the angle ∠APB. A tangent at point C meets the extensions of PA and PB at points Q and R, respectively. We are given the lengths QC = 3, QA = 2, and RC = 4, and we need to find the length of RB.
According to the Power of a Point theorem, for point P, we have:
PQ⋅PA=QC2
Let PQ = x. Then:
x⋅2=32
x⋅2=9
x=92
Using the sine rule in triangle PQR, we can relate the segments:
QCPQ=RCPR
Substituting the known values:
392=4PR
Cross-multiplying gives:
3⋅PR=4⋅92
3⋅PR=18
PR=6
Now, we apply the Power of a Point theorem again for triangle PCR:
PR⋅RB=RC2
Substituting the known values:
6⋅RB=42
6⋅RB=16
RB=166=83
Thus, the length of RB is:
83
Topper's Solved these Questions
- JEE MAIN - 5BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN - 5EXERCISE - PART III : MATHEMATICS (SECTION-2)
5 Videos
- INVERSE TRIGONOMETRYBOOK - VMC MODULES ENGLISHCHAPTER - INVERSE TRIGONOMETRYEXERCISE - JEE ADVANCED ( ARCHIVE )
10 Videos
- JEE MAIN REVISION TEST - 30 | JEE -2020BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 30 | JEE -2020EXERCISE - MATHEMATICS
25 Videos
Similar Questions
AB is the diameter and AC is a chord of a circle with centre O such that angle BAC=30∘. The tangent to the circle at C intersects AB produced in D. Show that BC=BD.
View SolutionFrom an external point P, two tangents, PA and PB are drawn to a circle with centre 0. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA=10 cm, find the perimeter of the triangle PCD.
View SolutionFrom an external point P, tangents PA and PB are drawn to a circle. CE is a tangent to the circle at D which intersect PA and PB at point E and C respectvely. If AP=15 cm, find the permeter of the △PEC.
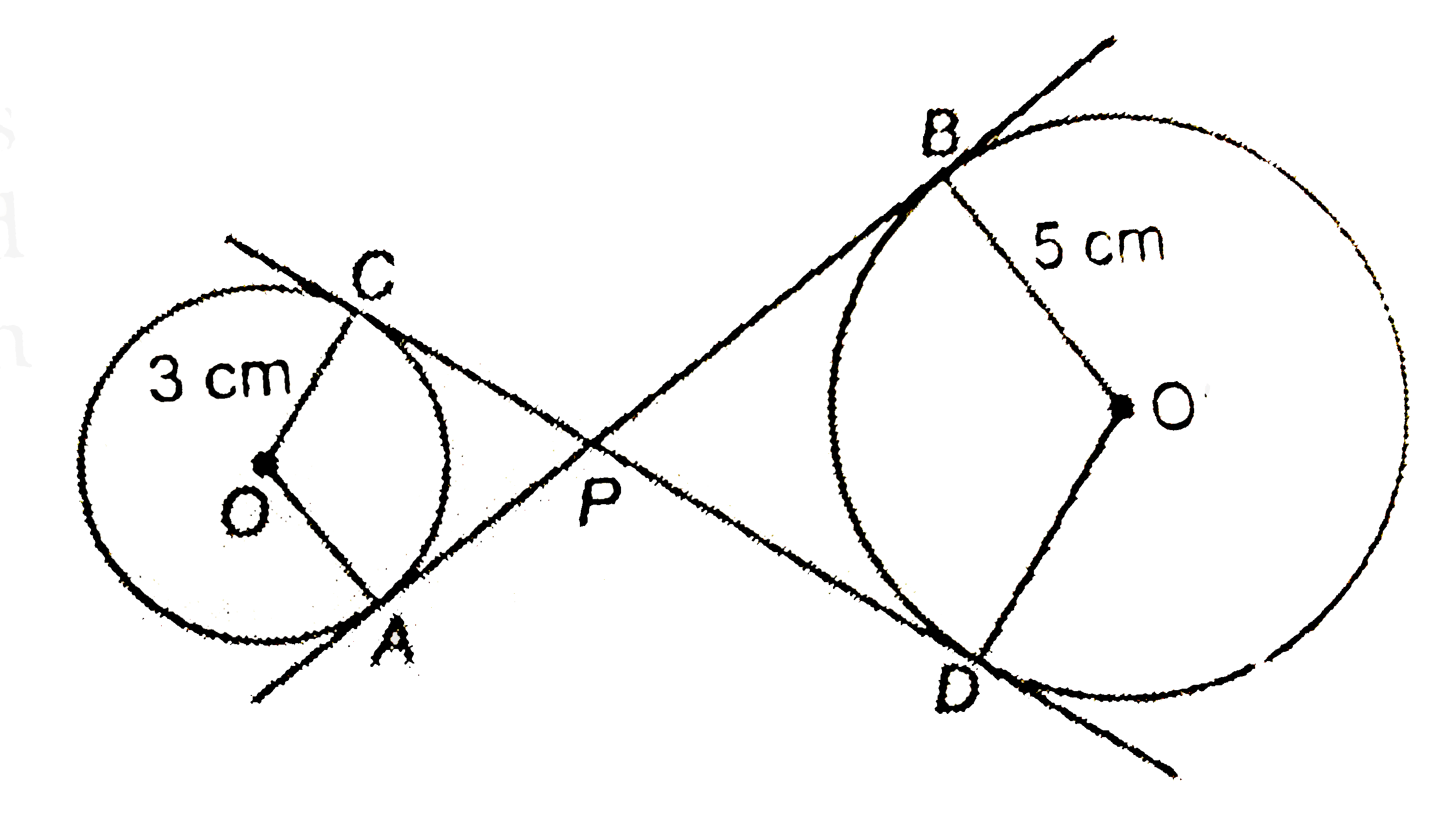
View SolutionIn figure, CPD and APB are common tangents to the two circles with centres O and O'. The radii of the two circles are 3 cm and 5 cm respectively. If AP:PB=1:3 and CP=4cm. Find the length of PB and OO'.
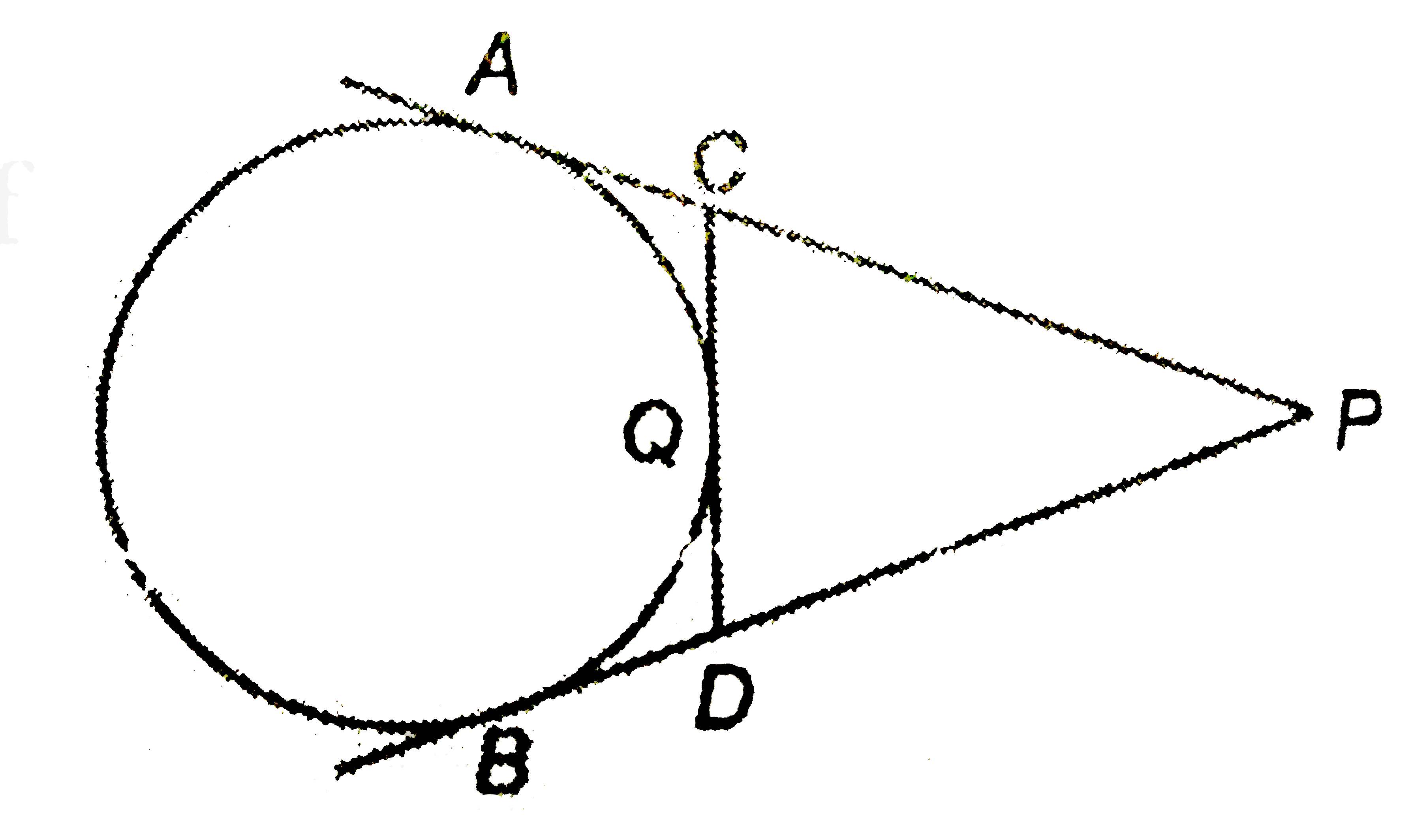
View SolutionPAandPB are tangents from P to the circle with centre O. At point M, a tangent is drawn cutting PA at K and PB at N. Prove that KN=AK+BN.
View SolutionIn the given figure PA and PB are tangents to the circle drawn from an external point P. CD is a third tangent touching the circle at Q. If PB=10cm and CQ=2cm. What is the length of PC?
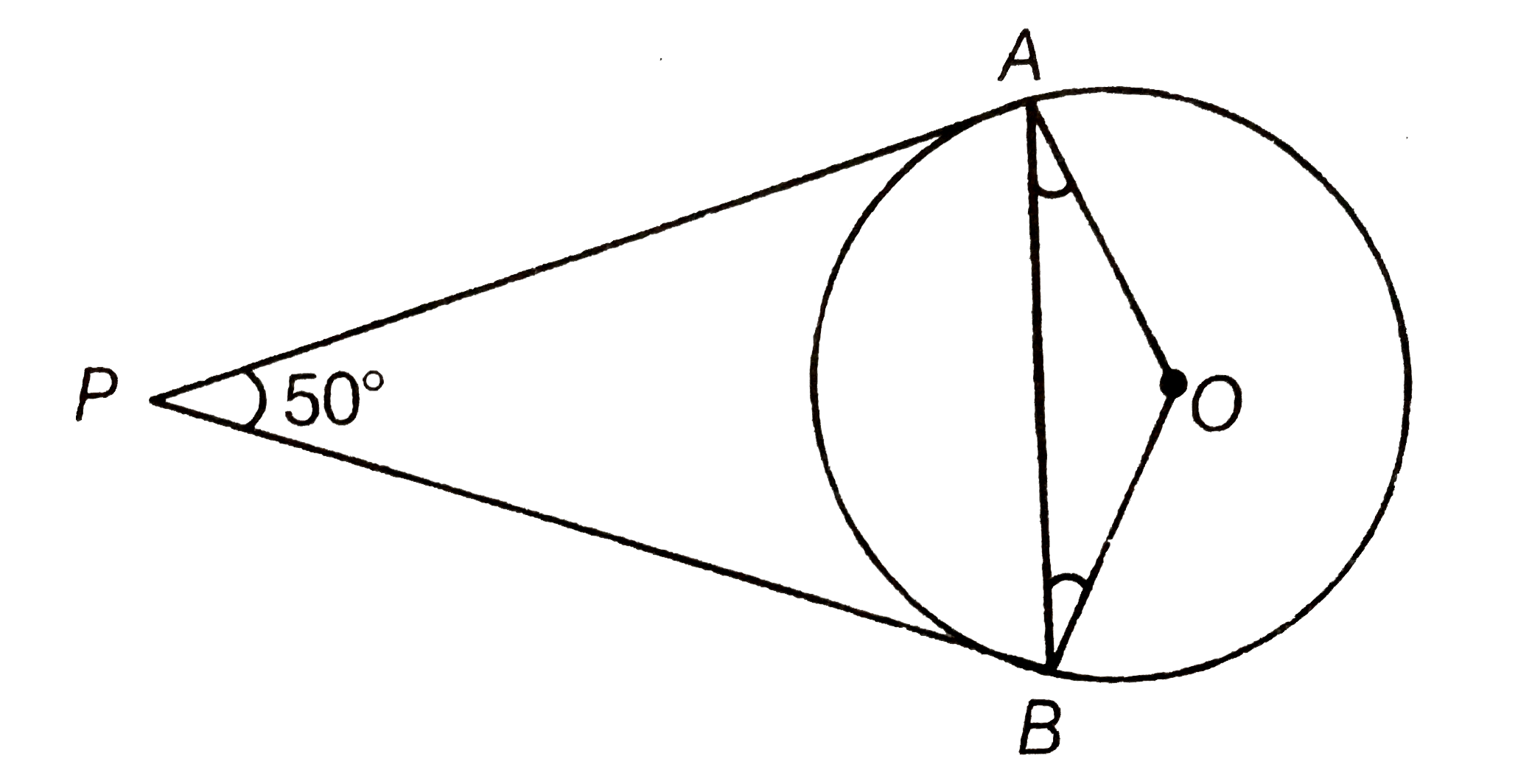
View SolutionIn figure, if PA and PB are tangents to the circle with centre O such that ∠APB=50∘, then ∠OAB is equal to
View SolutionAB and CD are two chords of a circle intersecting at a point P outside the circle. If
PA= 8cm, PC= 5cm and PD= 4cm, determine AB.
View SolutionPA and PB are tangents to a circle S touching it at points A and B. C is a point on S in between A and B as shown in the figure. LCM is a tangent to S intersecting PA and PB in S at points L and M, respectively. Then the perimeter of the triangle PLM depends on o
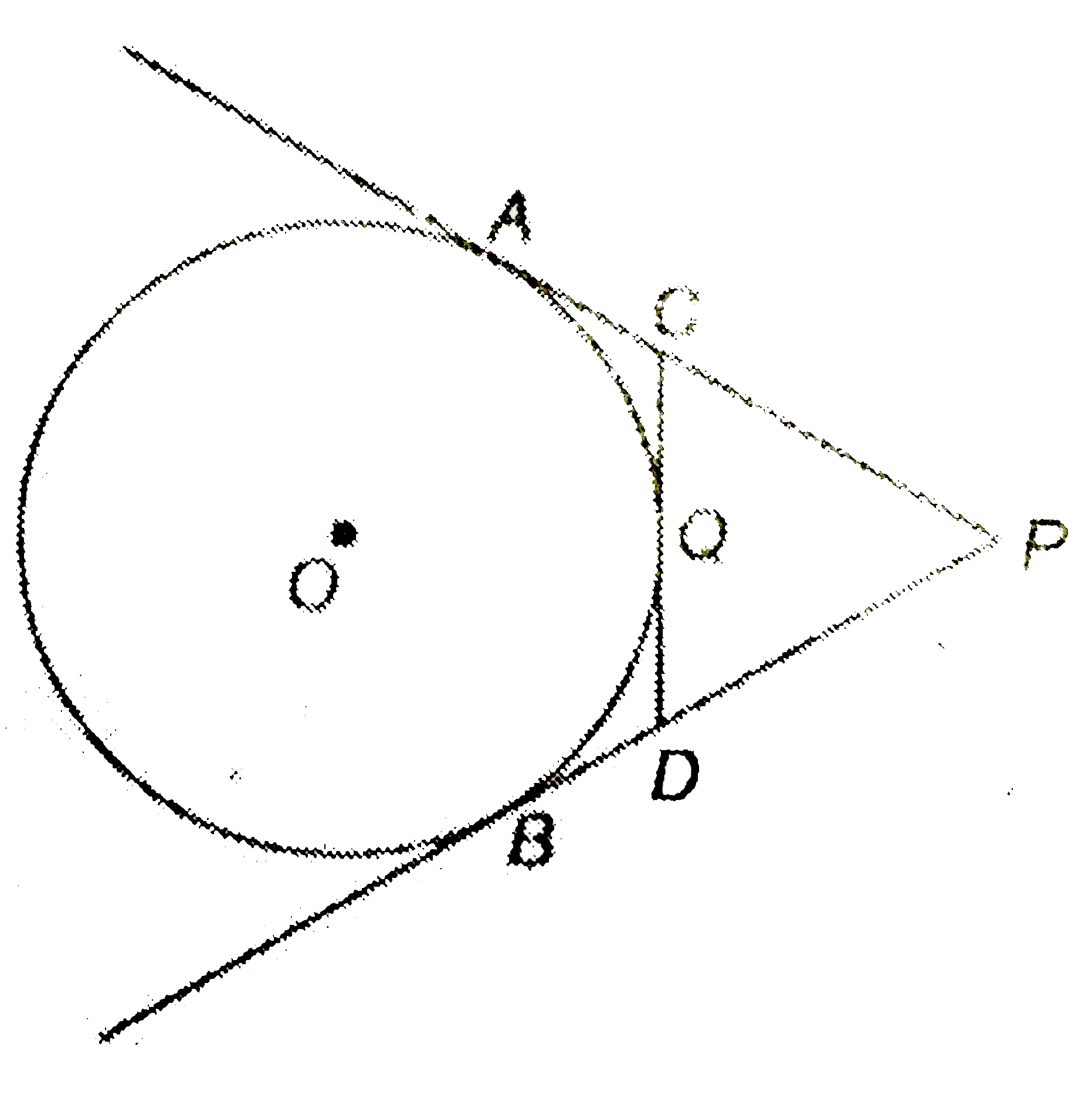
View SolutionIn the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA =12 cm, QC=3cm, then find PC+PD.
View Solution
