Let x1,x2,x3 be the points where f(x)=|1−|x−4∣∣,x∈R is not differentiable then f(x1)+f(x2)+f(x3)=
The correct Answer is:1
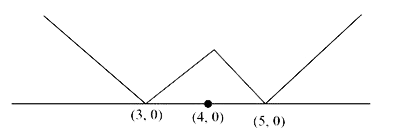
Function is not differentiable at x=3,4,5
So, f(3)+f(4)+f(5)
0+1+0=1
Topper's Solved these Questions
- MOCK TEST 11Book:VMC MODULES ENGLISHChapter:MOCK TEST 11Exercise:MATHEMATICS (Section-2)
Explore 5 Videos
- MOCK TEST 10Book:VMC MODULES ENGLISHChapter:MOCK TEST 10Exercise:MATHEMATICS (SECTION 2)
Explore 5 Videos
- MOCK TEST 12Book:VMC MODULES ENGLISHChapter:MOCK TEST 12Exercise:MATHEMATICS (SECTION 2)
Explore 5 Videos
Similar Questions
Let f(x)=||x|−1|, then points where, f(x) is not differentiable is/are
View SolutionLet f1(x)andf2(x) be twice differentiable functions where F(x)=f1(x)+f2(x)andG(x)=f1(x)−f2(x),∀x∈R,f1(0)=2andf2(0)=1.Iff'1(x)=f2(x)andf'2(x)=f1(x),∀x∈R then the number of solutions of the equation (F(x))2=9x4G(x)is...... .
View Solution
Knowledge Check
Let f(x) = x−[x],x∈R then f(12)is
A1B0C−1Dnone of these
If f(x)+2f(1−x)=x2+2∀x∈Randf(x) is a differentiable function, then the value of f'(8) is
View SolutionEvaluate ∫41f(x)dx, where f(x)=|x−1|+|x−2|+|x−3|.
View SolutionLet f1:R→R,f2:[0,∞)→R,f3:R→R be three function defined as
f1(x)={|x|x<0exx≥0,f2(x)=x2,f3(x)={f2(f1(x))x<0f2(f1(x))−1x≥0 then f3(x) is:
View SolutionIf f(x)={'x2(sgn[x])+{x},0≤x≤2''sinx+|x−3|,2<x<4, (where[.] & {.} greatest integer function & fractional part functiopn respectively ), then -
Option 1. f(x) is differentiable at x = 1
Option 2. f(x) is continuous but non-differentiable at x = 1
Option 3. f(x) is non-differentiable at x = 2
Option 4. f(x) is discontinuous at x = 2
View SolutionEvaluate ∫41f(x)dx, where f(x)=|x−1|+|x−2|+|x−3|
View SolutionLet f(x)=sin−1(2x1+x2)∀x∈R. The function f(x) is continuous everywhere but not differentiable at x is/ are
View SolutionLet f(x)=x2+x−1x2−x+1, then the largest value of f(x)∀x∈[−1,3] is:
View Solution
