Question

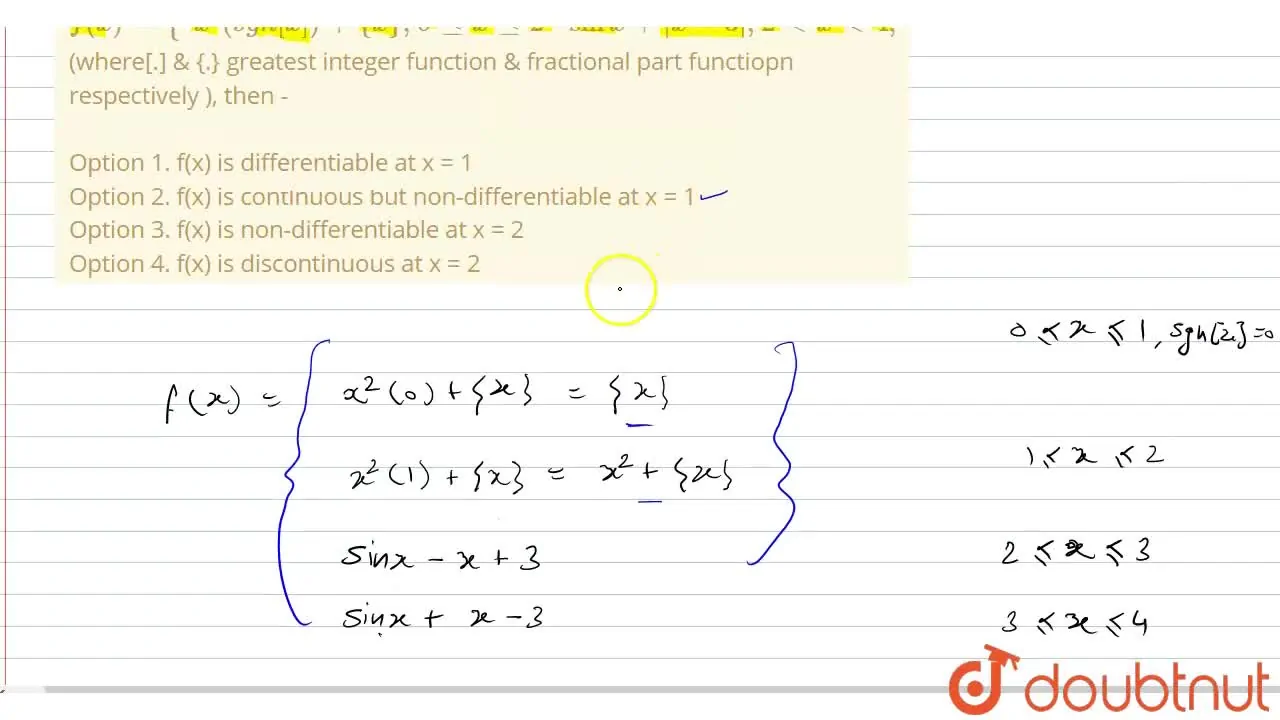
If $f\left(x\right)=\{\text{'}{x}^2\left(sgn\left[x\right]\right)+\left\{x\right\},0\le x\le 2\text{'}\text{'}\sin x+|x-3|,2<x<4,$ (where[.] & {.} greatest integer function & fractional part functiopn respectively ), then -

Option 1. f(x) is differentiable at x = 1
Option 2. f(x) is continuous but non-differentiable at x = 1
Option 3. f(x) is non-differentiable at x = 2
Option 4. f(x) is discontinuous at x = 2

Options

A. f(x) is differentiable at x = 1
B. f(x) is continuous but non-differentiable at x
C. f(x) is non-differentiable at x = 2
D. f(x) is discontinuous at x = 2

Answer

C::D

Explanation

To solve the problem, we need to analyze the piecewise function given by:

$$f\left(x\right)=\{\begin{array}{cc}{x}^2\cdot \text{sgn}\left(x\right)+\left\{x\right\},& 0\le x\le 2\\ \sin x+|x-3|,& 2<x<4\end{array}$$

where $$\text{sgn}\left(x\right)$$ is the signum function, $$\left(x\right)$$ is the greatest integer function, and $$\left\{x\right\}$$ is the fractional part function.

Step 1: Analyze \(f(x)\) for \(0 \leq x \leq 2\)

1. For \(0 \leq x < 1\):
- Here, \(\text{sgn}(x) = 0\) (since \(x\) is non-negative).
- Thus, \(f(x) = 0 + \{x\} = \{x\}\).
- The fractional part \(\{x\} = x\) since \(x\) is in \((0, 1)\).

2. For \(1 \leq x \leq 2\):
- Here, \(\text{sgn}(x) = 1\).
- Thus, \(f(x) = x^2 \cdot 1 + \{x\} = x^2 + \{x\}\).
- The fractional part \(\{x\} = x - 1\) for \(x \in (1, 2)\).

Therefore, for \(1 \leq x \leq 2\):
\( f(x) = x^2 + (x - 1) = x^2 + x - 1 \)

Step 2: Analyze \(f(x)\) for \(2 < x < 4\)

- For \(2 < x < 4\):
- We have \(f(x) = \sin x + |x - 3|\).
- For \(2 < x < 3\), \(|x - 3| = 3 - x\), so:
\( f(x) = \sin x + (3 - x) = \sin x + 3 - x \)
- For \(3 \leq x < 4\), \(|x - 3| = x - 3\), so:
\( f(x) = \sin x + (x - 3) = \sin x + x - 3 \)

Step 3: Check continuity at \(x = 1\)

- Calculate \(f(1)\):
\( f(1) = 1^2 + (1 - 1) = 1 + 0 = 1 \)

- Right-hand limit as \(x \to 1^+\):
\( \lim_{x \to 1^+} f(x) = f(1) = 1^2 + (1 - 1) = 1 \)

- Left-hand limit as \(x \to 1^-\):
\( \lim_{x \to 1^-} f(x) = \{1\} = 0 \)

Since the left-hand limit (0) does not equal the right-hand limit (1), \(f(x)\) is not continuous at \(x = 1\).

Step 4: Check differentiability at \(x = 1\)

Since \(f(x)\) is not continuous at \(x = 1\), it cannot be differentiable there.

Step 5: Check continuity at \(x = 2\)

- Calculate \(f(2)\):
\( f(2) = 2^2 + (2 - 1) = 4 + 1 = 5 \)

- Right-hand limit as \(x \to 2^+\):
\( \lim_{x \to 2^+} f(x) = \sin(2) + |2 - 3| = \sin(2) + 1 \)

- Left-hand limit as \(x \to 2^-\):
\( \lim_{x \to 2^-} f(x) = 2^2 + (2 - 1) = 5 \)

Since \(\sin(2) + 1 \neq 5\), \(f(x)\) is not continuous at \(x = 2\).

Conclusion:

- \(f(x)\) is not continuous at \(x = 1\) and \(x = 2\).
- \(f(x)\) is non-differentiable at \(x = 1\) and \(x = 2\).

Final Answer:

- Option 2: \(f(x)\) is continuous but non-differentiable at \(x = 1\) is incorrect.
- Option 3: \(f(x)\) is non-differentiable at \(x = 2\) is correct.
- Option 4: \(f(x)\) is discontinuous at \(x = 2\) is correct.