The logical statement (~q⇒~p)∨(~q⇒p) is equivalent to :
A
p→q
B
q→p
C
:(:p→q)
D
Tautology
Video Solution
Text Solution
The correct Answer is:D
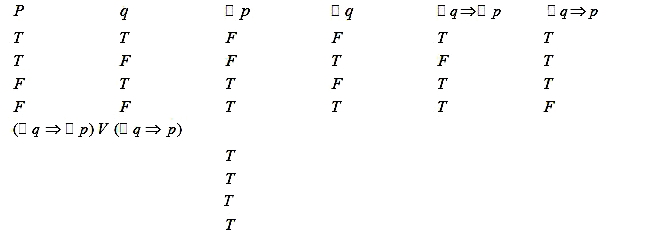
It.s is a tautology .
|
Topper's Solved these Questions
- MOCK TEST 11Book:VMC MODULES ENGLISHChapter:MOCK TEST 11Exercise:MATHEMATICS (Section-2)
Explore 5 Videos
- MOCK TEST 10Book:VMC MODULES ENGLISHChapter:MOCK TEST 10Exercise:MATHEMATICS (SECTION 2)
Explore 5 Videos
- MOCK TEST 12Book:VMC MODULES ENGLISHChapter:MOCK TEST 12Exercise:MATHEMATICS (SECTION 2)
Explore 5 Videos
Similar Questions
The logical statement (p→q)∨(q→~p) is :
View SolutionIf p and q are logical statements, then p⇒(~q⇒p) is equivalent to
View SolutionThe statement p∨q is
View SolutionThe logical statement [~(~p∨q)∨(p∧r)]∧(~q∧r) is equivalent to (a) (~p∧~q)∧r (b) ~p∨r (c) (p∧r)∧~q (d) (p∧~q)∨r
View Solution~(p∨q)∨(~p∧q) is equivalent to
View SolutionThe statement ~(p∧q)∨q
View Solutionp→q is logically equivalent to
View Solutionp∧(q∧r) is logically equivalent to
View SolutionIf p and q are two logical statements, then ~(p∨q)→(p→q) is equivalent to
View SolutionThe statement p→(q→p) is equivalent to
View Solution