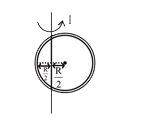
The radius of gyration of a uniform circular ring of radius R, about an axis which is a chord of circle of length $\sqrt{3} R$ is ,

A

$\frac{R}{2}$

B

$\frac{\sqrt{3} R}{2}$

C

$\frac{2 R}{\sqrt{3}}$

D

$\frac{R}{\sqrt{3}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$I = I_{c m} + m {(\frac{R}{2})}^{2}$
$\Rightarrow I = \frac{M R^{2}}{2} + \frac{M R^{2}}{4}$
$\Rightarrow I = \frac{M R^{2}}{2} + \frac{M R^{2}}{4}$
$\Rightarrow I = \frac{3}{4} M R^{2}$
$∴ M R^{2} = \frac{3}{4} M R^{2} \Rightarrow R = \frac{\sqrt{3} R}{2}$

|

Updated on:21/07/2023

Class 12 PHYSICS MOCK TEST 9

Topper's Solved these Questions

Similar Questions

VMC MODULES ENGLISH-MOCK TEST 9-PHYSICS (SECTION 2)

Home
Ask Doubt
Profile