Aray of light falls on one side of a prism whose refracting angle is 75∘. Find the angle of incidence in order that the emergent ray may just graze the other side, (μ=√2)
To solve the problem of finding the angle of incidence for a ray of light falling on a prism with a refracting angle of 75∘ such that the emergent ray just grazes the other side, we can follow these steps:
Step 1: Understand the condition for grazing
The emergent ray grazing the other side of the prism means that the angle of refraction at the second surface of the prism is 90∘. This is because a ray grazing the surface will not enter the medium beyond the prism.
Step 2: Use the concept of critical angle
The angle of refraction being 90∘ indicates that the angle of incidence at the second surface must be equal to the critical angle. The critical angle C can be calculated using the formula:
C=sin−1(1μ)
Given that the refractive index μ=√2, we can find the critical angle:
C=sin−1(1√2)=45∘
Step 3: Relate angles in the prism
Let A be the refracting angle of the prism, R1 be the angle of refraction at the first surface, and R2 be the angle of refraction at the second surface. According to the prism formula:
A=R1+R2
Since R2=90∘, we can substitute:
75∘=R1+90∘
This gives:
R1=75∘−90∘=−15∘
However, we need to consider that R2 should be 45∘ (the critical angle). Thus:
R1+45∘=75∘
This leads to:
R1=75∘−45∘=30∘
Step 4: Apply Snell's Law
Using Snell's Law at the first surface, we have:
μ1sinI=μ2sinR1
Where μ1=1 (for air) and μ2=√2. Substituting the values:
1⋅sinI=√2⋅sin30∘
Since sin30∘=12, we can substitute:
sinI=√2⋅12=√22
Step 5: Calculate the angle of incidence
Now, we find I:
I=sin−1(√22)=45∘
Final Answer
Thus, the angle of incidence I required for the emergent ray to just graze the other side of the prism is:
45∘
The emergent ray grazing the other side of the prism means that the angle of refraction at the second surface of the prism is 90∘. This is because a ray grazing the surface will not enter the medium beyond the prism.
The angle of refraction being 90∘ indicates that the angle of incidence at the second surface must be equal to the critical angle. The critical angle C can be calculated using the formula:
C=sin−1(1μ)
Given that the refractive index μ=√2, we can find the critical angle:
C=sin−1(1√2)=45∘
Let A be the refracting angle of the prism, R1 be the angle of refraction at the first surface, and R2 be the angle of refraction at the second surface. According to the prism formula:
A=R1+R2
Since R2=90∘, we can substitute:
75∘=R1+90∘
This gives:
R1=75∘−90∘=−15∘
However, we need to consider that R2 should be 45∘ (the critical angle). Thus:
R1+45∘=75∘
This leads to:
R1=75∘−45∘=30∘
Using Snell's Law at the first surface, we have:
μ1sinI=μ2sinR1
Where μ1=1 (for air) and μ2=√2. Substituting the values:
1⋅sinI=√2⋅sin30∘
Since sin30∘=12, we can substitute:
sinI=√2⋅12=√22
Now, we find I:
I=sin−1(√22)=45∘
Thus, the angle of incidence I required for the emergent ray to just graze the other side of the prism is:
45∘
Topper's Solved these Questions
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - Example
21 Videos
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - PRACTICE EXERCISE-1
1 Videos
- QUIZBOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS
30 Videos
- RAY OPTICS AND WAVE OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS AND WAVE OPTICS EXERCISE - IMPECCABLE
58 Videos
Similar Questions
Calculate the angle of incidence on the face of a prism of refracting angle 60∘ and of refractive index 1.5, for which the emergent ray just grazes the other face.
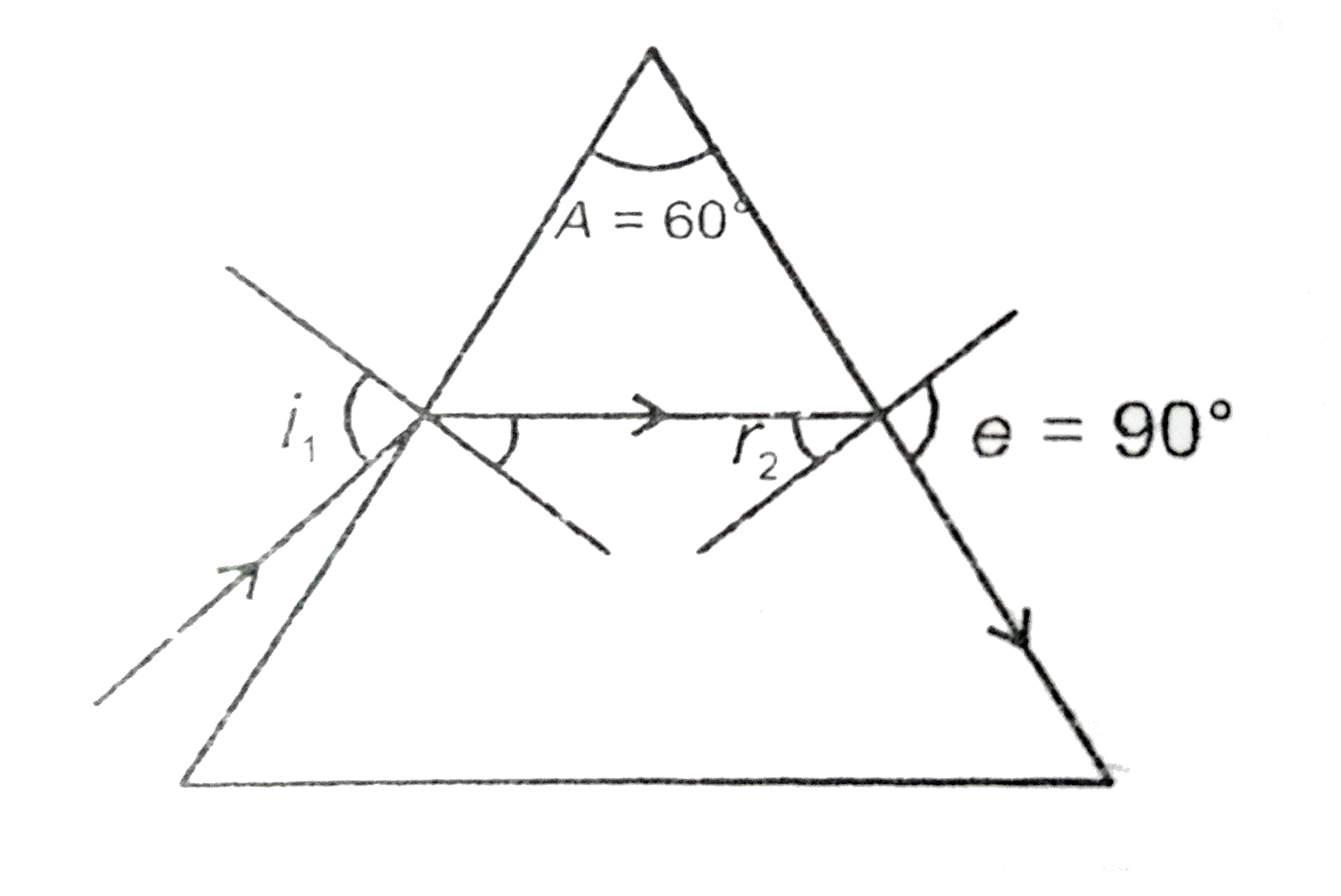
View SolutionLight ray is incident on a prism of angle A=60∘ are refractive index μ=√2. The angle of incidence which the emergent rays grazes the surface is given
View Solution
Knowledge Check
A ray of light passes through an equilateral prism (refractive index 1.5) such that angle of incidence is equal to angle of emergence and the latter is equal to 3/4th of the angle of prism. Calculate the angle of deviation.
A60∘B30∘C45∘D120∘
A ray of light falls on a normally on a refracting face of a prism. Find the angle of prism if the ray just fails to emerge from the prism (μ=3/2).
View SolutionA ray of light is incident on a prism whose refractive index is 1.52 at an angle of 40∘. If the angle of emergence is 60∘, calculate the angle of the prism.
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionFor a ray of light refracted through a prism of angle 60∘, the angle of incidence is equal to the angle of emergence, each equal to 45∘. Find the refractive index of the material of the prism.
View SolutionA ray of light suffers a minimum deviation when incident on equilateral prism of refractive index √2 The angle of deviation is
View SolutionA ray of light is incident on one face of a prism (m=√3) at an angle of 60∘. The refracting angle of the prism is also 60∘. Find the angle of emergence .

View Solution
