A ray of light is travelling at an angle of 20° above the horizontal. At what angle with the horizontal must a plane mirror be placed in its path so that it becomes vertically upward after reflection.
To solve the problem of determining the angle at which a plane mirror must be placed so that a ray of light traveling at an angle of 20° above the horizontal reflects vertically upward, we can follow these steps:
1. Understanding the Incident Ray:
- The ray of light is traveling at an angle of 20° above the horizontal. This means that the angle of the incident ray with respect to the horizontal line is 20°.
2. Setting Up the Mirror:
- We need to place a plane mirror at an angle (let's call it θ') with respect to the horizontal. The normal to the mirror will be perpendicular to the surface of the mirror.
3. Identifying Angles:
- The angle of incidence (i) is the angle between the incident ray and the normal to the mirror. Since the incident ray is at 20° above the horizontal, if the mirror is at an angle θ' to the horizontal, then the angle of incidence can be expressed as:
i=20°−θ′
4. Reflection Condition:
- For the ray to reflect vertically upward, the angle of reflection (r) must be 90°. According to the law of reflection, the angle of incidence is equal to the angle of reflection:
r=i
- Therefore, we have:
90°=20°−θ′(since r=i)
5. Solving for θ':
- Rearranging the equation:
θ′=20°−90°
θ′=−70°
- Since angles are measured positively from the horizontal, we take the absolute value:
θ′=70°
6. Final Adjustment:
- However, we need to consider that the mirror is placed at an angle θ' with respect to the horizontal. Therefore, the angle of the mirror with respect to the horizontal must be:
θ′=90°−20°=70°
Conclusion:
The angle at which the plane mirror must be placed with respect to the horizontal is 70°.
- The ray of light is traveling at an angle of 20° above the horizontal. This means that the angle of the incident ray with respect to the horizontal line is 20°.
- We need to place a plane mirror at an angle (let's call it θ') with respect to the horizontal. The normal to the mirror will be perpendicular to the surface of the mirror.
- The angle of incidence (i) is the angle between the incident ray and the normal to the mirror. Since the incident ray is at 20° above the horizontal, if the mirror is at an angle θ' to the horizontal, then the angle of incidence can be expressed as:
i=20°−θ′
- For the ray to reflect vertically upward, the angle of reflection (r) must be 90°. According to the law of reflection, the angle of incidence is equal to the angle of reflection:
r=i
- Therefore, we have:
90°=20°−θ′(since r=i)
- Rearranging the equation:
θ′=20°−90°
θ′=−70°
- Since angles are measured positively from the horizontal, we take the absolute value:
θ′=70°
- However, we need to consider that the mirror is placed at an angle θ' with respect to the horizontal. Therefore, the angle of the mirror with respect to the horizontal must be:
θ′=90°−20°=70°
The angle at which the plane mirror must be placed with respect to the horizontal is 70°.
Topper's Solved these Questions
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - Example
21 Videos
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - PRACTICE EXERCISE-1
1 Video
- QUIZBOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS
30 Videos
- RAY OPTICS AND WAVE OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS AND WAVE OPTICS EXERCISE - IMPECCABLE
58 Videos
Similar Questions
A light ray is incident on a plane mirror at an angle of 30∘ with horizontal. At what angle with horizontal must a plane mirror be placed in its path so that it becomes vertically upwards after reflection?
View SolutionOn a plane mirror, a ray of light is incident at an angle of 30∘ with horizontal . To make the reflected ray vertical , at what angle with horizontal must a plane mirror be placed ?

View Solutionrays of light strike a horizontal plane mirror at an angle of 45∘. At what angle should be a second plane mirror be placed in order that the reflected ray finally be reflected horizontally from the second mirror.
View SolutionWhen a ray of light strikes a plane mirror along the normal, the angle of incidence is :
View SolutionA ray of light makes an angle of 10∘ with the horizontal and strikes a plane mirror which is inclined at an angle θ to the horizontal. The angle θ for which the reflected ray becomes vertical, is
View SolutionA ray of light is incident at an angle of 30∘ with the plane of a plane mirror. Find the angle of reflection.
View SolutionRays of light are incident on a plane mirror at 40∘. At what angle with the first should a second mirror be placed such that the rays emerge from the second mirror parallel to the first mirror.
View SolutionA particle is projected with a velocity of 20ms−1 at an angle of 60∘ to the horizontal. The particle hits the horizontal plane again during its journey. What will be the time of impact ?
View SolutionA block is placed on a smooth inclined plane at an angle 'θ' to the horizontal. The acceleration must the plane be moved horizontally so that the block to fall freely is
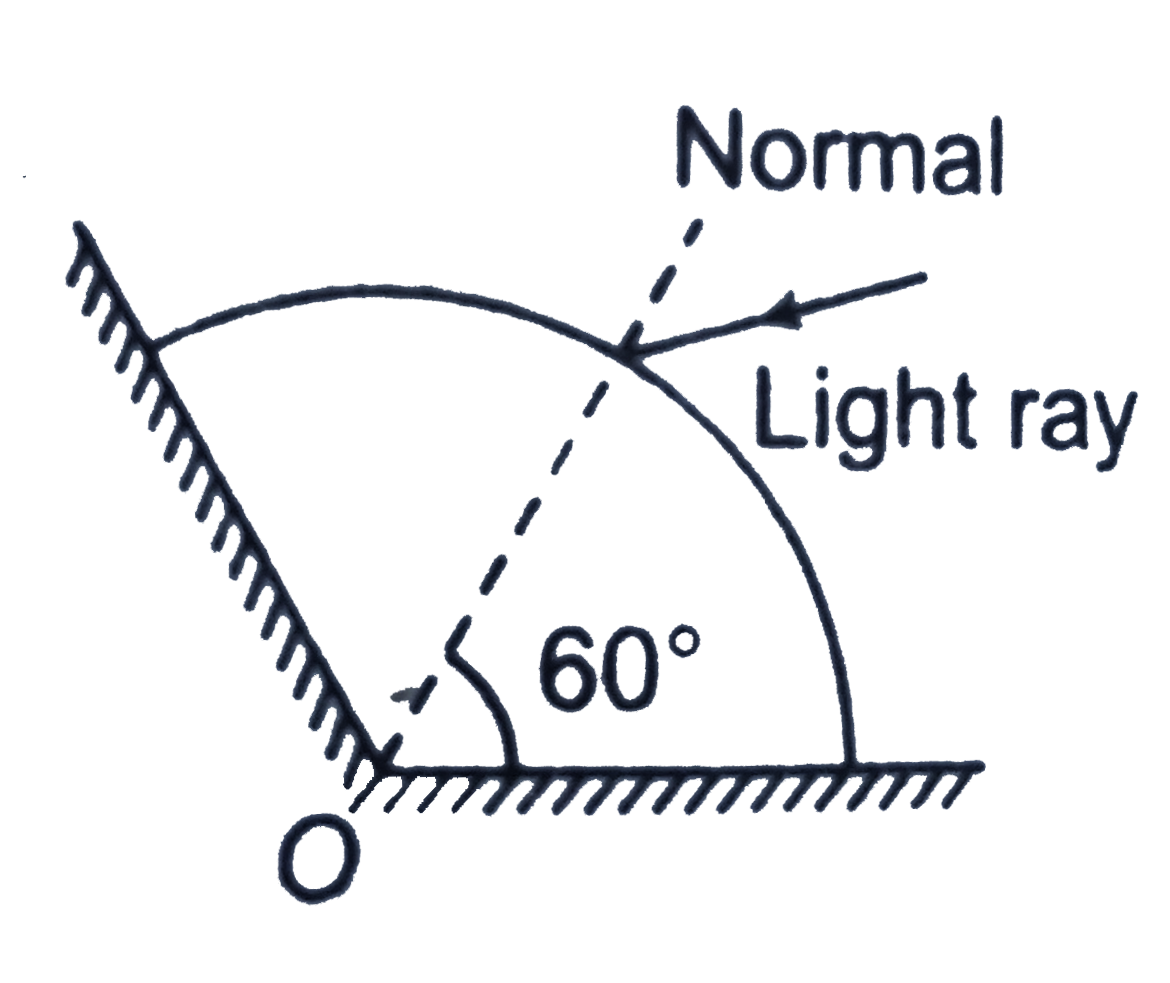
View SolutionConsider the situation as shown in figure. The point O is the centre. The light ray forms an angle of 60∘ with the horizontal and each mirror makes an angle 60∘ with the normal. The value of refractive index of that spherical portion so that light ray retraces its path is
View Solution
