The velocities of three particles of masses 20 g, 30 g and 50 g are 10ˆi, 10ˆj and 10ˆk respectively. The velocity of the centre of mass of the three particles is
To find the velocity of the center of mass (COM) of the three particles, we can follow these steps:
1. Identify the Masses and Velocities:
- Mass of particle 1, m1=20g with velocity →v1=10^im/s
- Mass of particle 2, m2=30g with velocity →v2=10^jm/s
- Mass of particle 3, m3=50g with velocity →v3=10^km/s
2. Write the Formula for Velocity of Center of Mass:
The velocity of the center of mass →VCOM is given by:
→VCOM=m1→v1+m2→v2+m3→v3m1+m2+m3
3. Substitute the Values into the Formula:
→VCOM=20^i⋅10+30^j⋅10+50^k⋅1020+30+50
4. Calculate Each Component:
- For the ^i component:
20⋅10=200^i
- For the ^j component:
30⋅10=300^j
- For the ^k component:
50⋅10=500^k
5. Combine the Components:
→VCOM=200^i+300^j+500^k100
6. Divide by the Total Mass:
→VCOM=200100^i+300100^j+500100^k
→VCOM=2^i+3^j+5^k
7. Final Result:
The velocity of the center of mass is:
→VCOM=2^i+3^j+5^km/s
8. Magnitude of the Velocity of Center of Mass:
To find the magnitude:
|→VCOM|=√(2)2+(3)2+(5)2=√4+9+25=√38m/s
- Mass of particle 1, m1=20g with velocity →v1=10^im/s
- Mass of particle 2, m2=30g with velocity →v2=10^jm/s
- Mass of particle 3, m3=50g with velocity →v3=10^km/s
The velocity of the center of mass →VCOM is given by:
→VCOM=m1→v1+m2→v2+m3→v3m1+m2+m3
→VCOM=20^i⋅10+30^j⋅10+50^k⋅1020+30+50
- For the ^i component:
20⋅10=200^i
- For the ^j component:
30⋅10=300^j
- For the ^k component:
50⋅10=500^k
→VCOM=200^i+300^j+500^k100
→VCOM=200100^i+300100^j+500100^k
→VCOM=2^i+3^j+5^k
The velocity of the center of mass is:
→VCOM=2^i+3^j+5^km/s
To find the magnitude:
|→VCOM|=√(2)2+(3)2+(5)2=√4+9+25=√38m/s
Topper's Solved these Questions
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF A PARTICLES & ROTATIONAL MOTIONExercise:PRACTICE EXERCISE-2
Explore 5 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF A PARTICLES & ROTATIONAL MOTIONExercise:PRACTICE EXERCISE-3
Explore 5 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF A PARTICLES & ROTATIONAL MOTIONExercise:SOLVED EXAMPLES
Explore 20 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:7-previous year question
Explore 46 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:IMPECCABLE
Explore 56 Videos
Similar Questions
The coordinates of the centre of mass of a system of three particles of mass 1g,2g and 3g are (2,2,2). Where should a fourth particle of mass 4 g be positioned so that the centre of mass of the four particle system is at the origin of the three-dimensional coordinate system ?
View SolutionTwo particles whose masses are 10 kg and 30 kg and their position vectors are ˆi+ˆj+ˆkand−ˆi−ˆj−ˆk respectively would have the centre of mass at position :-
View Solution
Knowledge Check
Two bodies of masses 10kgand2kg are moving with velocities (2ˆi−7ˆj+3ˆk)and(−10ˆi+35ˆj−3ˆk)m/s respectively. Calculate the velocity of their centre of mass.
A1. 2ˆims−1B2. 2ˆkms−1C3. (2ˆj+2ˆk)ms−1D4. (2ˆi+2ˆj+2ˆk)ms−1
Two bodies of 6kg and 4kg masses have their velocity 5ˆi−2ˆj+10ˆk and 10ˆi−2ˆj+5ˆk respectively. Then, the velocity of their centre of mass is
View SolutionThree particles of masses 1.0 kg 2.0 kg and 3.0 kg are placed at the corners A,B and C respectively of an equilateral triangle ABC of edge 1m. Locate the centre of mass of the system.
View SolutionThree particles of masses 0.50 kg, 1.0 kg and are placed at the corners of a right angle triangle, as shown in fig. Locate the centre of mass of the system.
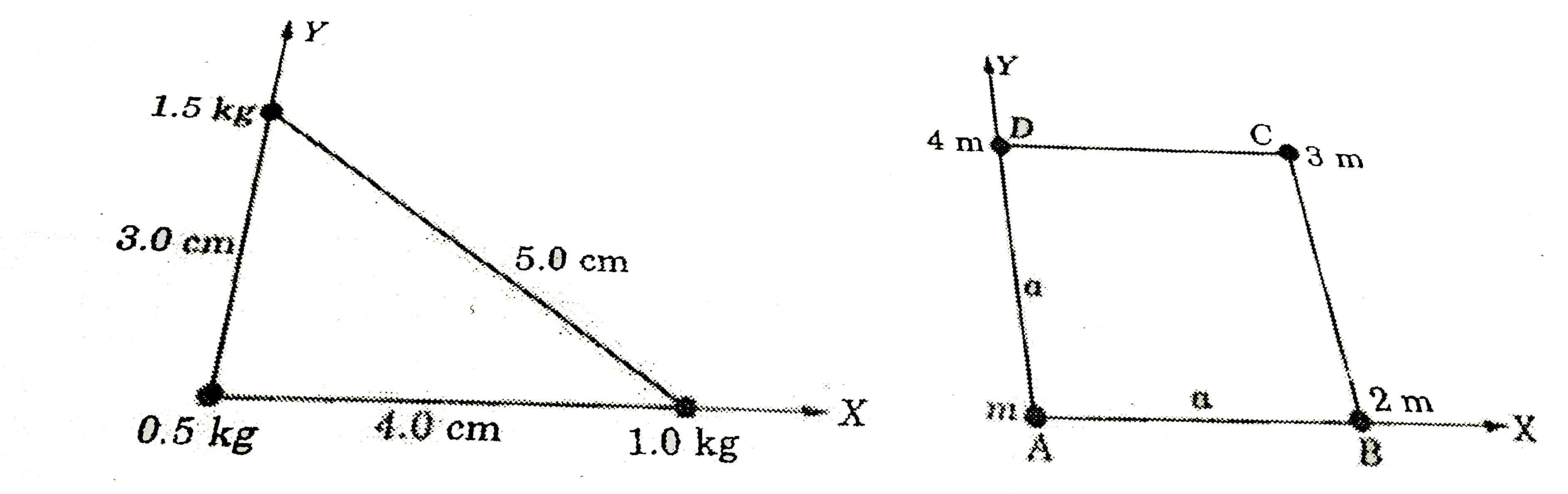
View Solution(b) Two bodies of masses 10kg and 2 kg are moving with velocities 2ˆi−7ˆj+3ˆk and −10ˆi+35ˆj−3ˆkm/s respectively. Find the velocity of the centre of mass.
View SolutionIn a certain experiments to measure the ratio of charge to mass of elementry particles, a surprising result was obtained in which two particle, a surprising result was obtained in which two particles moved in such a way that the distance between them always remained constant. It was also noticed that this two-particle system was isolated from all other particles and no force was acting on this system except the force between these two mases. After careful observation followed bu intensive calculation, it was deduced that velocity of these two particles was always opposite in direction and magnitude of velocity was 103ms−1and2×103ms−1 for first and second particle, respectively, and mass of these particles were 2×10−30kgand10−30kg, respectively. Distance between them were 12Å(1Å = 10^(-10)m).
if the first particle is stopped for a moment and then released, the velocity of center of mass of the system just after the release will be
View SolutionA Diwali cracker of mass 60 g at rest, explodes into three pieces A, B and C of mass 10 g, 20 g and 30 g respectively. After explosion velocities of A and B are 30 m/s along east and 20 m/s along north respectively. The instantaneous velocity of C will be
View SolutionThree particles of masses 20g, 30g and 40g are initially moving along the positive direction of the three coordinate axes respectively with the same velocity of 20cm/s. When due to their mutual interaction, the first particle comes to rest, the second acquires a velocity (10ˆi+20ˆk)cm/s. What is then the velocity of the third particle?
View Solution