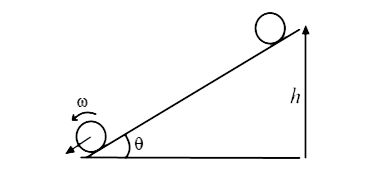
A solid cylinder of radius r rolls down an inclined plane of height $h$ and inclination $θ$ . Calculate its speed at the bottom of the plane using energy method. Also calculate the time taken to reach of the bottom.

Video Solution

Text Solution

Verified by Experts

Energy Method : Let $V_{c m}, ω$ CO be the velocity of centre of mass and the angular velocity of cylinder respectively at the bottom of the plane.As the cylinder rolls down without rubbing, NO energy is lost due to friction as heat.Loss in GP.E.=gain in KE $m g h = \frac{1}{2} m V_{C m}^{2} + \frac{1}{2} I ω^{2}$ As the cylinder is rolling without slipping, $V_{C M} = R ω$ $\Rightarrow m g h = \frac{1}{2} m V_{C M}^{2} + (\frac{1}{2} \frac{m R^{2}}{2}) (\frac{V_{C M}^{2}}{R^{2}})$ $\Rightarrow V_{C M} = \sqrt{\frac{4 g h}{3}}$ Acceleration Method : From the result of last illustration (using $k^{2} = \frac{R^{2}}{2}$ ) Acceleration of the cylinder is $\frac{g sin θ}{1 + \frac{1}{2}} = \frac{2}{3} g sin θ$ Using $V_{V M}^{2} = 0^{2} + 2 A_{C M} S$ as down the plane (taking downward directionpositive) $\Rightarrow v = \sqrt{0 + 2 a \frac{h}{sin θ}} = \sqrt{2 (\frac{2}{3} g sin θ) \frac{h}{sin θ}} = \sqrt{\frac{4 g h}{3}}$ Time to reach bottom= $= \frac{v - 0}{a} = \frac{\sqrt{(\frac{4 g h}{3}) - 0}}{\frac{2}{3} g sin θ} = \sqrt{\frac{3 h}{g}} \frac{1}{sin θ}$ .

Updated on:21/07/2023

|

Class 12 PHYSICS SYSTEM OF A PARTICLES & ROTATIONAL MOTION

Topper's Solved these Questions

Similar Questions

VMC MODULES ENGLISH-SYSTEM OF A PARTICLES & ROTATIONAL MOTION-IN-CHAPTER EXERCISE F

Home
Ask Doubt
Profile