Find the moment of inertia of a uniform ring of mass M and radius R about a diameter.

Video Solution

Text Solution

Verified by Experts

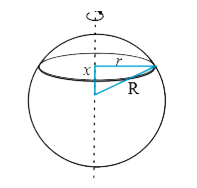
The sphere may be divided into disks perpendicular to the given axis, as shown in fig. The disk at a distance x from the center of the sphere has a radius $r = {(R^{2} - x^{2})}^{\frac{1}{2}}$ and a thickness dr. If $ρ = \frac{M}{V}$ is the volume mass density (mass perunit volume), the mass of this elemental disk is $d m = ρ d V = p π r^{2} d x,$ or $d m = ρ π (R^{2} - x^{2}) d x$ From the last example, the moment of inertia of this elemental disk is $d I = \frac{1}{2} d m r^{2} = \frac{1}{2} ρ π (R^{2} - x^{2}) d x$ The total moment of inertia is $I = \frac{1}{2} ρ π \int_{- R}^{R} (R^{4} - 2 R^{2} x^{2} + x^{4}) d x$ $= \frac{1}{2} ρ π {[R^{4} x - \frac{2}{3} R^{2} x^{3} + \frac{1}{5} x^{5}]}_{- R}^{4} = \frac{8}{15} ρ π R^{5}$ The total mass of the sphere is $M = ρ (\frac{4}{3} π R^{3})$ , so the moment of inertia maybe written as : $I = \frac{2}{5} M R^{2}$ .

|

Updated on:21/07/2023

Class 12 PHYSICS SYSTEM OF A PARTICLES & ROTATIONAL MOTION

Topper's Solved these Questions

Similar Questions

VMC MODULES ENGLISH-SYSTEM OF A PARTICLES & ROTATIONAL MOTION-IN-CHAPTER EXERCISE F

Home
Ask Doubt
Profile