A body of mass 2 kg lying on a smooth surface is attached to a string 3 m long and then rotated in a horizontal circle making 60 rev/min. Calculate the centripetal acceleration.
To solve the problem of calculating the centripetal acceleration of a body rotating in a horizontal circle, we can follow these steps:
Step 1: Convert the angular velocity from revolutions per minute (rev/min) to radians per second (rad/s).
Given:
- Angular velocity, ω=60rev/min
To convert revolutions per minute to radians per second, we use the conversion factor:
- 1rev=2πradians
- 1min=60seconds
So, we calculate ω as follows:
ω=60rev/min×2πradians1rev×1min60s=2πrad/s
Step 2: Use the formula for centripetal acceleration.
The formula for centripetal acceleration ac is given by:
ac=ω2⋅r
where r is the radius of the circular path.
Given:
- Length of the string (radius), r=3m
Step 3: Substitute the values into the formula.
Substituting ω=2πrad/s and r=3m into the centripetal acceleration formula:
ac=(2π)2⋅3
Step 4: Calculate (2π)2.
Calculating (2π)2:
(2π)2=4π2
Step 5: Substitute back to find ac.
Now substituting 4π2 back into the equation:
ac=4π2⋅3=12π2
Step 6: Approximate π2 for final calculation.
Using π2≈10:
ac≈12⋅10=120m/s2
Final Answer:
The centripetal acceleration is approximately 120m/s2.
---
- Angular velocity, ω=60rev/min
- 1rev=2πradians
- 1min=60seconds
ω=60rev/min×2πradians1rev×1min60s=2πrad/s
ac=ω2⋅r
where r is the radius of the circular path.
- Length of the string (radius), r=3m
ac=(2π)2⋅3
(2π)2=4π2
ac=4π2⋅3=12π2
ac≈12⋅10=120m/s2
The centripetal acceleration is approximately 120m/s2.
Topper's Solved these Questions
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:SOLVED EXAMPLES
Explore 20 Videos
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:PRACTICE EXERCISE
Explore 80 Videos
- MOTION IN A STRAIGHT LINE & PLANE Book:VMC MODULES ENGLISHChapter:MOTION IN A STRAIGHT LINE & PLANE Exercise:IMPECCABLE
Explore 52 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:MCQ
Explore 2 Videos
Similar Questions
A string breaks under a load of 4.8kg A mass of 0.5 kg is attached to one end of a string 2 m long and is rotated in a horizontal circle . Calculate the greatest number of revolutions that the mass can make without breaking the string .
View SolutionA mass is tied to a, string 1 m long and rotated in a horizontal circle at the rate of 600 rpm. If the tension inthe string is 3943.8 N, calculate the mass.
View SolutionA stone of mass 0.1 kg tied to one end of a string lm long is revolved in a horizontal circle at the rate of 10π rev/s. Calculate the tension in the string.
View SolutionA metal bob of mass 0.6 kg is attached to the end of a string of length 1 m and the bob is whirled in a horizontal circle with a uniform speed of 12 m/s. What is the centripetal force acting on the bob ? If the speed of the bob is 5 m/s calculate the tension in the string.
View SolutionA stone of mass 100 g tied to the end of a string 80 cm long is whirled in a horizontal circle with a constant speed.If the stone makes 14 revolutions in 25 s, calculate the centripetal force acting on the stone.
View SolutionA stone of mass of 16 kg is attached to a string 144 m long and is whirled in a horizontal circle. The maximum tension the string can withstand is 16 Newton . The maximum velocity of revolution that can be given to the stone without breaking it, will be
View SolutionA 2 kg mass placed on a level table and is attached by a string passing over the edge of a table as illustrated in the diagram.
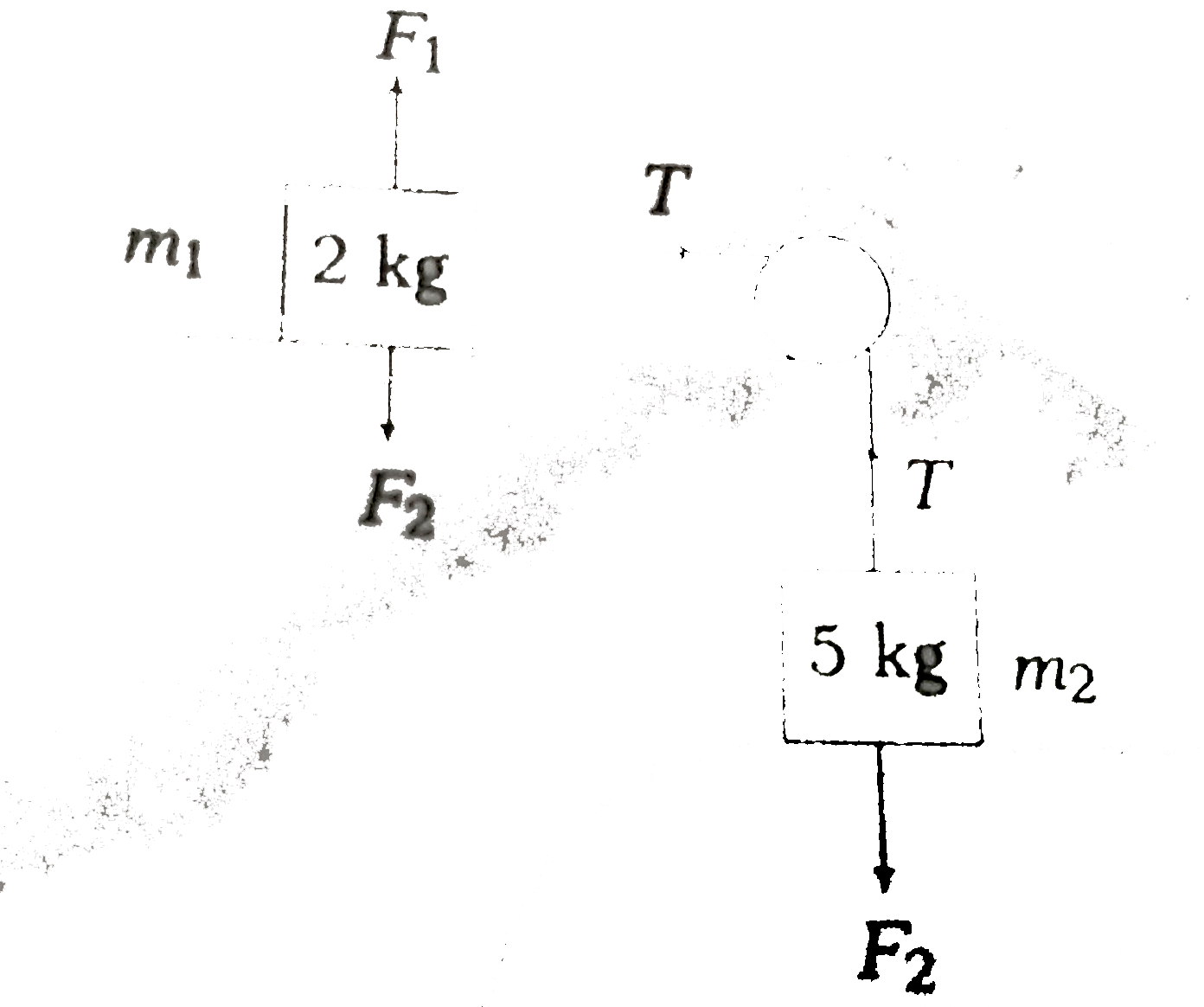
(i) Calculate the magnitude of acceleration of the system.
(ii) Calculate the tension in the string.
View SolutionA stone tied to the end of a string 80 cm long is whirled in a horizontal circle with a constant speed. If the centripetal acceleration of the stone is 9.91ms−2 how many revolutions does the stone make in 20 seconds.
View SolutionA stone of mass 2.0 kg is tied to the end of a string of 2m length. It is whirled in a horizontal circle. If the breaking tension of the string is 400 N, calculate the maximum velocity of the stone.
View SolutionA mass of 100 gm is tied to one end of a string 2 m long. The body is revolving in a horizontal circle making a maximum of 200 revolutions per min. The other end of the string is fixed at the centre of the circle of revolution. The maximum tension that the string can bear is (approximately)
View Solution

