A very broad elevator is going up vertically with a constant acceleration of 2m/s2. At the instant when its velocity is 4m/s a ball is projected form the floor of the lift with a speed of 4m/s relative to the floor at an elevation of 30∘. Time taken by the ball to return the floor is (g=10ms2)
2√3m
√3m
2√3m
2m
To solve the problem step by step, we will analyze the motion of the ball projected from the elevator.
Step 1: Understand the situation
The elevator is moving upward with a constant acceleration of 2m/s2 and has a velocity of 4m/s at the moment the ball is projected. The ball is projected at an angle of 30∘ with a speed of 4m/s relative to the elevator's floor.
Step 2: Determine the effective acceleration of the ball
The ball experiences two accelerations:
1. The gravitational acceleration g=10m/s2 acting downward.
2. The upward acceleration of the elevator a=2m/s2.
The effective acceleration of the ball relative to the elevator is:
arelative=g−a=10m/s2−2m/s2=8m/s2 (downward)
Step 3: Resolve the initial velocity of the ball
The initial velocity of the ball can be resolved into vertical and horizontal components:
- Vertical component uy=4sin(30∘)=4⋅12=2m/s
- Horizontal component ux=4cos(30∘)=4⋅√32=2√3m/s
Step 4: Apply the second equation of motion in the vertical direction
Using the second equation of motion for vertical displacement, we set the final displacement s=0 when the ball returns to the floor of the elevator:
s=uyt+12arelativet2
Substituting the known values:
0=2t+12(−8)t2
This simplifies to:
0=2t−4t2
Step 5: Factor the equation
Factoring out t:
t(2−4t)=0
This gives us two solutions:
1. t=0 (the time at which the ball is projected)
2. 2−4t=0⇒t=12 seconds
Step 6: Conclusion
The time taken by the ball to return to the floor of the elevator is t=12seconds.
The elevator is moving upward with a constant acceleration of 2m/s2 and has a velocity of 4m/s at the moment the ball is projected. The ball is projected at an angle of 30∘ with a speed of 4m/s relative to the elevator's floor.
The ball experiences two accelerations:
1. The gravitational acceleration g=10m/s2 acting downward.
2. The upward acceleration of the elevator a=2m/s2.
arelative=g−a=10m/s2−2m/s2=8m/s2 (downward)
The initial velocity of the ball can be resolved into vertical and horizontal components:
- Vertical component uy=4sin(30∘)=4⋅12=2m/s
- Horizontal component ux=4cos(30∘)=4⋅√32=2√3m/s
Using the second equation of motion for vertical displacement, we set the final displacement s=0 when the ball returns to the floor of the elevator:
s=uyt+12arelativet2
Substituting the known values:
0=2t+12(−8)t2
This simplifies to:
0=2t−4t2
Factoring out t:
t(2−4t)=0
This gives us two solutions:
1. t=0 (the time at which the ball is projected)
2. 2−4t=0⇒t=12 seconds
The time taken by the ball to return to the floor of the elevator is t=12seconds.
Topper's Solved these Questions
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - PRACTICE EXERCISE
80 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-A
11 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-J
10 Videos
- MOTION IN A STRAIGHT LINE & PLANE BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - IMPECCABLE
52 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
Similar Questions
An elecator is going up with an upward acceleration of 1m/s2. At the instant when its velocity is 2m/s, a stone is projected upward from its floor with a speed of 2m/s relative to the elevator, at an elevation of 30∘.
(a) Calculate the time taken by the stone to return to the floor.
(b) Sketch the path of the projectile as observed by an observer outside the elevator.
(c) If the elevator was moving with a downward acceleration equal to g, how would the motion be altered?
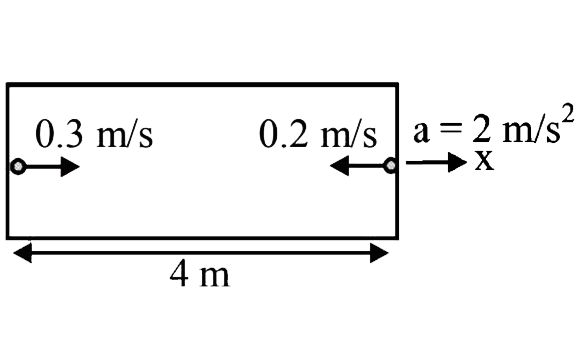
View SolutionA rocket is moving in a gravity free space with a constant acceleration of 2m/s2 along +x direction (see figure). The length of a chamber inside the rocket is 4m. A ball is thrown from the left end of the chamber in +x direction with a speed of 0.3m/s relative to the rocket . At the same time , another ball is thrown in +x direction with a speed of 0.2m/s drom its right end relative to the rocket . The time in seconds when the two balls hit each other is
View Solution
Knowledge Check
A girl standing on a stationary lift (open from above) throws a ball upwards with initial speed 50ms−1. The time taken by the ball to return to her hands is (Take g = 10ms−2)
Aa. 5 sBb. 10 sCc. 15 sDd. 20 sA cricket ball is thrown at a speed of 30 m s−1 in a direction 30∘ above the horizontal. The time taken by the ball to return to the same level is
A2 sB3 sC4 sD5 s
An elevator ascends an upward acceleration of 0.2 m/s2. At the instant it upwards speed in 3m/sec a loose bolt 5 m high form the floor drops from the ceiling of the elevator.Find the time until the bolt strikes the floor and the displacement it has fallen .
View SolutionStarting from rest, A lift moves up with an acceleration of 2ms−2. In this lift , a ball is dropped from a height of 1.5m (with respect to floor of lift). The time taken by the ball to reach the floor of the lift is (g=10ms−2)
View SolutionA 60 kg man stands on an elevator floor The elevator is going up with constant acceleration of 1.96 m/s2. Percentage change in the apparent weight of the person is
View SolutionAn elevator (lift) ascends with an upward acceleration of 1.2ms−2. At the instant when its upward speed is 2.4ms−1, a loose bolt drops from the ceiling of the elevator 2.7m above the floor of the elevator. Calculate (a) the time of flight of the bolt from the ceiling to the floor and (b) the distance it has fallen relaative to the elevator shaft.
View SolutionA particle is projected from a horizontal floor with speed 10m/s at an angle 30∘ with the floor and striking the floor after sometime. State which is correct.
View SolutionA coin is released inside a lift at a height of 2m from the floor of the lift. The height of the lift is 10 m. The lift is moving with an acceleration of 9m/s2downwards. The time after which the coin will strike with the lift is : (g=10m/s2)
View Solution

