A train running at 30 m/s is slowed uniformly to stop in 44 s. Find the acceleration and the stopping distance.
To solve the problem step by step, we will find the acceleration and the stopping distance of the train.
Step 1: Identify the given values
- Initial velocity (u) = 30 m/s (the speed of the train before it starts to slow down)
- Final velocity (v) = 0 m/s (the speed of the train when it stops)
- Time (t) = 44 s (the time taken to stop)
Step 2: Calculate the acceleration
We can use the formula for acceleration when the initial and final velocities and time are known:
v=u+at
Rearranging this formula to solve for acceleration (a):
a=v−ut
Substituting the known values:
a=0−3044
a=−3044
This simplifies to:
a=−1522 m/s2
The negative sign indicates that this is a deceleration (retardation).
Step 3: Calculate the stopping distance
To find the stopping distance (s), we can use the formula:
v2=u2+2as
Rearranging to solve for s:
s=v2−u22a
Substituting the known values:
s=02−3022×(−1522)
Calculating 302:
s=−9002×(−1522)
This simplifies to:
s=−900−3022
s=900×2230
s=900×2230=900×1115
Calculating further:
s=60×22=1320 m
Thus, the stopping distance is:
s=660 m
Final Answers
- Acceleration (a) = −1522 m/s2
- Stopping distance (s) = 660 m
---
- Initial velocity (u) = 30 m/s (the speed of the train before it starts to slow down)
- Final velocity (v) = 0 m/s (the speed of the train when it stops)
- Time (t) = 44 s (the time taken to stop)
We can use the formula for acceleration when the initial and final velocities and time are known:
v=u+at
Rearranging this formula to solve for acceleration (a):
a=v−ut
Substituting the known values:
a=0−3044
a=−3044
This simplifies to:
a=−1522 m/s2
The negative sign indicates that this is a deceleration (retardation).
To find the stopping distance (s), we can use the formula:
v2=u2+2as
Rearranging to solve for s:
s=v2−u22a
Substituting the known values:
s=02−3022×(−1522)
Calculating 302:
s=−9002×(−1522)
This simplifies to:
s=−900−3022
s=900×2230
s=900×2230=900×1115
Calculating further:
s=60×22=1320 m
Thus, the stopping distance is:
s=660 m
- Acceleration (a) = −1522 m/s2
- Stopping distance (s) = 660 m
Topper's Solved these Questions
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - SOLVED EXAMPLES
20 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - PRACTICE EXERCISE
80 Videos
- MOTION IN A STRAIGHT LINE & PLANE BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - IMPECCABLE
52 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
Similar Questions
A particle moves in a circular path of radius 0.5m at a speed that uniformly increases. Find the angular acceleration of particle if its speed changes from 2.0m/s to 4.0m/s in 4.0s
View SolutionA particle moves in a circular path of radius 0.5m at a speed that uniformly increases. Find the angular acceleration of particle if its speed changes from 2.0m/s to 4.0m/s in 4.0s
View SolutionA car is moving with a velocity of 10 m/s. Suddenly driver sees a child at a distance of 30 m and he applies the brakes, it produced a uniform retardation in car and car stops in 5 second. Find (mass of car=1000 kg)
the stopping distance of car
will the car hit the child
the retardation in car
resistive force on car
View SolutionA subway train travels between two of its stations at then stops with the acceleration shcedule shown in the acceleration versus time graph. Then
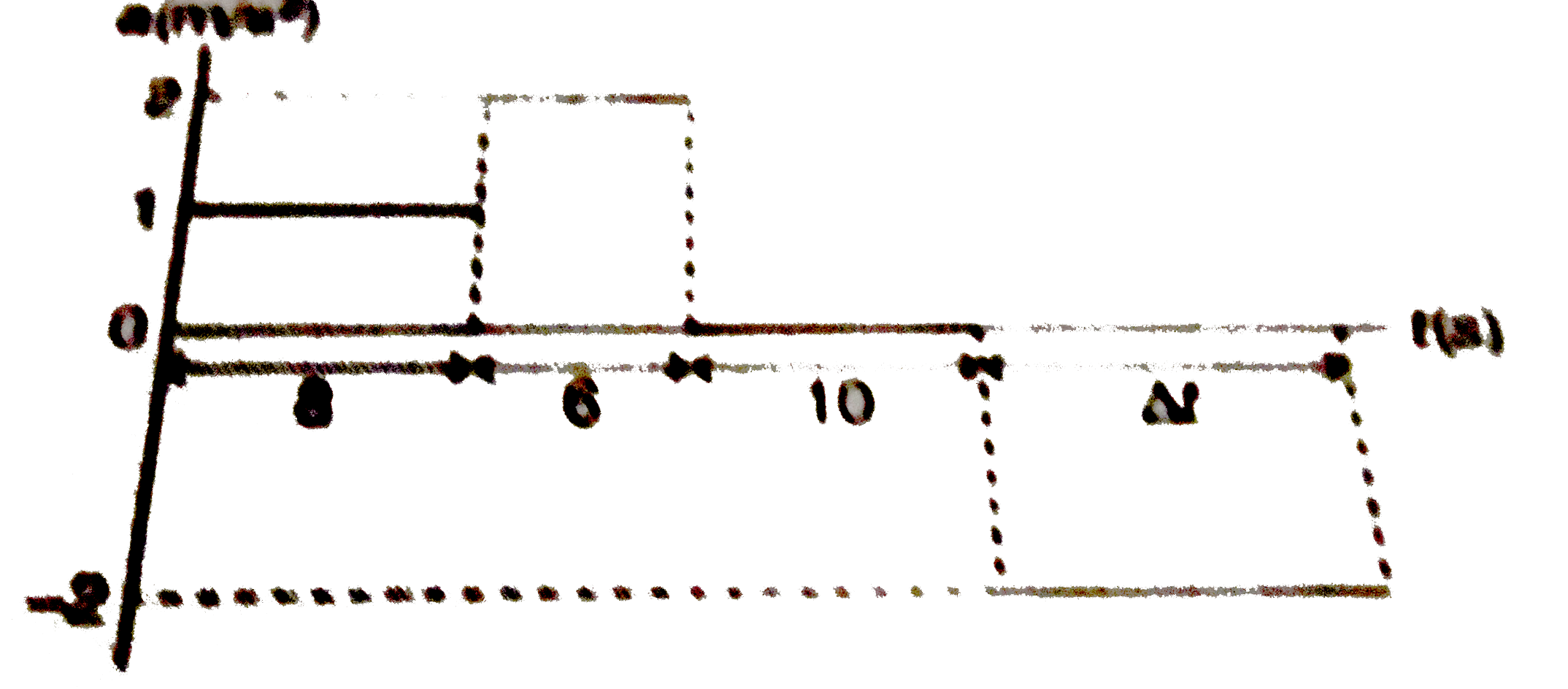
View SolutionA toy car initially moving with uniform velocity of 18km h−1 comes to a stop in 2 s. Find the retardation of the car in S.I. units.
View SolutionA car travelling with a velocity of 80 km/h slowed down to 44 km/h in 15 s. The retardation is
View SolutionA car travelling with a velocity of 80 km/h slowed down to 44 km/h in 15 s. The retardation is
View SolutionAn express train moving at 30 m/s reduces its speed to 10 m/s in a distance of 240 m. If the breaking force is increased by 12.5% in the beginning find the distance that it travels before coming to rest
View SolutionA motor car running at the rate of 7m/s can be stopped by brakes in 10m. Prove that the total resistance to the motion when the brakes are on is one-fourth of the weight of the car.
View SolutionIf a car at rest, accelerates uniformly to a speed of 144km/h in 20s, it covers a distance of
View Solution
