A queen is placed at the centre of carom-board which has side of length a . It is hit from a position with a striker such that after rebounding from the front end, it goes into the hole in the opposite end. Find the distance traveled by the queen
To solve the problem of finding the distance traveled by the queen on a carom board, we can follow these steps:
Step 1: Understand the Setup
The queen is placed at the center of a square carom board with side length a. When hit by a striker, it rebounds off the front edge and moves towards the hole at the opposite end.
Step 2: Define the Coordinates
Let's define the coordinates:
- The center of the carom board (where the queen is placed) is at (a/2,a/2).
- The front edge (where the striker hits) can be considered as the line y=0.
- The hole at the opposite end is at (a/2,a).
Step 3: Determine the Path of the Queen
When the queen is hit, it travels to the front edge and then rebounds towards the hole. The path can be visualized as a straight line from the center to the front edge, and then another straight line from the front edge to the hole.
Step 4: Calculate the Distances
1. Distance d1: The distance from the center of the board to the point where it hits the front edge.
- The vertical distance from the center to the front edge is a/2.
- The horizontal distance can be denoted as x0.
- Using the Pythagorean theorem, we can express d1 as:
d1=√(a/2)2+x20
2. Distance d2: The distance from the point of impact on the front edge to the hole.
- The vertical distance from the front edge to the hole is a.
- The horizontal distance remains x0.
- Using the Pythagorean theorem again, we can express d2 as:
d2=√(a)2+x20
Step 5: Use Similar Triangles
From the geometry of the situation, we can set up a relationship using similar triangles:
a/2d1=ad2
This leads to:
d2=2d1
Step 6: Solve for x0
Using the relationship derived from similar triangles:
2d1=d2
Substituting the expressions for d1 and d2:
2√(a/2)2+x20=√(a)2+x20
Step 7: Square Both Sides and Solve
Squaring both sides gives:
4(a24+x20)=a2+x20
This simplifies to:
4x20+a2=a2+x20
Thus:
3x20=0⟹x0=a6
Step 8: Calculate d1
Substituting x0 back into the equation for d1:
d1=√(a2)2+(a6)2=√a24+a236=√9a2+a236=√10a236=a√106
Step 9: Calculate Total Distance
The total distance traveled by the queen is:
D=d1+d2=d1+2d1=3d1=3⋅a√106=a√102
Final Answer
The distance traveled by the queen is:
D=a√102
The queen is placed at the center of a square carom board with side length a. When hit by a striker, it rebounds off the front edge and moves towards the hole at the opposite end.
Let's define the coordinates:
- The center of the carom board (where the queen is placed) is at (a/2,a/2).
- The front edge (where the striker hits) can be considered as the line y=0.
- The hole at the opposite end is at (a/2,a).
When the queen is hit, it travels to the front edge and then rebounds towards the hole. The path can be visualized as a straight line from the center to the front edge, and then another straight line from the front edge to the hole.
1. Distance d1: The distance from the center of the board to the point where it hits the front edge.
- The vertical distance from the center to the front edge is a/2.
- The horizontal distance can be denoted as x0.
- Using the Pythagorean theorem, we can express d1 as:
d1=√(a/2)2+x20
- The vertical distance from the front edge to the hole is a.
- The horizontal distance remains x0.
- Using the Pythagorean theorem again, we can express d2 as:
d2=√(a)2+x20
From the geometry of the situation, we can set up a relationship using similar triangles:
a/2d1=ad2
This leads to:
d2=2d1
Using the relationship derived from similar triangles:
2d1=d2
Substituting the expressions for d1 and d2:
2√(a/2)2+x20=√(a)2+x20
Squaring both sides gives:
4(a24+x20)=a2+x20
This simplifies to:
4x20+a2=a2+x20
Thus:
3x20=0⟹x0=a6
Substituting x0 back into the equation for d1:
d1=√(a2)2+(a6)2=√a24+a236=√9a2+a236=√10a236=a√106
The total distance traveled by the queen is:
D=d1+d2=d1+2d1=3d1=3⋅a√106=a√102
The distance traveled by the queen is:
D=a√102
Topper's Solved these Questions
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - SOLVED EXAMPLES
20 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - PRACTICE EXERCISE
80 Videos
- MOTION IN A STRAIGHT LINE & PLANE BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - IMPECCABLE
52 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
Similar Questions
An object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
the position of the image
View SolutionFind the equation of the circle whose radius is 5 and centre lies on the positive side of x-axis at a distance 5 from the origin.
View SolutionA carrom board (4ft×4ft) has the queen at the centre. The queen hit by the striker moves to the front edge, rebounds and goes in the hole behind the striking line. Find the magnitude of displacement of the queen a. from the centre to the front edge b. from the front edge to the hole and c. from the centre to the hole.
View SolutionA rod is of length 3 m and its mass acting per unit length is directly proportional to distance x from its one end. The centre of gravity of the rod from that end will be at
View SolutionThe density of a rod of length L varies as ρ=A+Bx where x is the distance from the left end. Locate the centre of mass.

View SolutionA rod of length L is of non uniform cross-section. Its mass per unit length varies linearly with distance from left end. Then its centre of mass from left end is at a distance. (Take linear density at left end=0).
View SolutionA closed organ pipe of length L is in resonance with a tuning fork. If a hole is made in the pipe at a distance L4 from closed - end, it will be in resonance again, when:
View SolutionTwo particles A and B of mass m each hit the ends of a rigid bar of mass M and length l inelastically from opposite sides the speeds v and perpendicular to the rod. The bar is kept on a smooth horizontal plane (as shown). Find the linear and angular speed of the system (bar+particle).

View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to the rod.

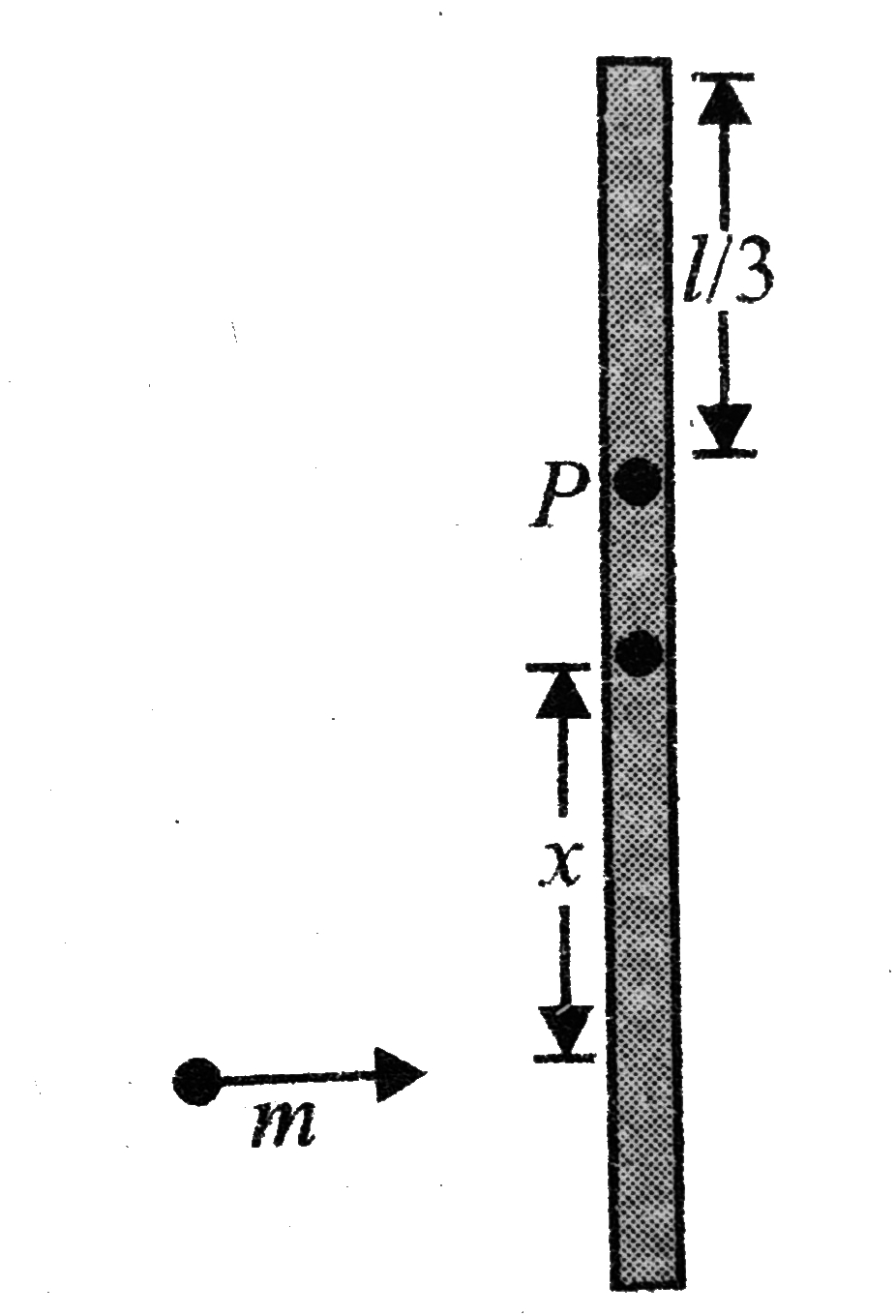
View SolutionA thin uniform rod of mass m and length l is kept on a smooth horizontal surface such that it can move freely. At what distance from centre of rod should a particle of mass m strike on the rod such that the point P at a distance l3 from the end of the rod is instantaneously at rest just after the elastic collision?
View Solution
