The period P of a simple pendulum is the time for one complete swing. How does P depend on the mass m of the bob, the length l of the string, and the acceleration due to gravity g?
To determine how the period P of a simple pendulum depends on the mass m of the bob, the length l of the string, and the acceleration due to gravity g, we can use dimensional analysis. Here’s a step-by-step solution:
Step 1: Identify the variables
The variables involved are:
- P: the period of the pendulum (time)
- m: the mass of the bob (mass)
- l: the length of the string (length)
- g: the acceleration due to gravity (length/time²)
Step 2: Set up the relationship
We assume a relationship of the form:
P=k⋅ma⋅lb⋅gc
where k is a dimensionless constant, and a, b, and c are the powers to be determined.
Step 3: Write the dimensions of each variable
The dimensions of the variables are:
- (P)=T (time)
- (m)=M (mass)
- (l)=L (length)
- (g)=LT2 (acceleration)
Step 4: Substitute dimensions into the equation
Substituting the dimensions into the equation gives:
(T)=(k)⋅(M)a⋅(L)b⋅(LT2)c
Since k is dimensionless, we can ignore its dimensions.
Step 5: Expand the dimensions
This expands to:
(T)=(M)a⋅(L)b+c⋅(T)−2c
Step 6: Compare dimensions
Now we compare the dimensions on both sides:
- For time T: 1=−2c
- For mass M: 0=a
- For length L: 1=b+c
Step 7: Solve the equations
From 1=−2c:
c=−12
From 0=a:
a=0
From 1=b+c:
1=b−12⟹b=32
Step 8: Write the final relationship
Substituting the values of a, b, and c back into the equation for P:
P=k⋅m0⋅l32⋅g−12
This simplifies to:
P=k⋅l32⋅g−12
Step 9: Final expression
Thus, the period P of a simple pendulum is given by:
P=k√l3g
The variables involved are:
- P: the period of the pendulum (time)
- m: the mass of the bob (mass)
- l: the length of the string (length)
- g: the acceleration due to gravity (length/time²)
We assume a relationship of the form:
P=k⋅ma⋅lb⋅gc
where k is a dimensionless constant, and a, b, and c are the powers to be determined.
The dimensions of the variables are:
- (P)=T (time)
- (m)=M (mass)
- (l)=L (length)
- (g)=LT2 (acceleration)
Substituting the dimensions into the equation gives:
(T)=(k)⋅(M)a⋅(L)b⋅(LT2)c
Since k is dimensionless, we can ignore its dimensions.
This expands to:
(T)=(M)a⋅(L)b+c⋅(T)−2c
Now we compare the dimensions on both sides:
- For time T: 1=−2c
- For mass M: 0=a
- For length L: 1=b+c
From 1=−2c:
c=−12
a=0
1=b−12⟹b=32
Substituting the values of a, b, and c back into the equation for P:
P=k⋅m0⋅l32⋅g−12
This simplifies to:
P=k⋅l32⋅g−12
Thus, the period P of a simple pendulum is given by:
P=k√l3g
Topper's Solved these Questions
- UNITS, MEASUREMENTS & ERRORSBook:VMC MODULES ENGLISHChapter:UNITS, MEASUREMENTS & ERRORSExercise:SOLVED EXAMPLES
Explore 20 Videos
- UNITS, MEASUREMENTS & ERRORSBook:VMC MODULES ENGLISHChapter:UNITS, MEASUREMENTS & ERRORSExercise:PRACTICE EXERCISE - 1
Explore 11 Videos
- UNITS, MEASUREMENTS & ERRORSBook:VMC MODULES ENGLISHChapter:UNITS, MEASUREMENTS & ERRORSExercise:Impeccable
Explore 51 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:IMPECCABLE
Explore 56 Videos
- WAVE MOTIONBook:VMC MODULES ENGLISHChapter:WAVE MOTIONExercise:JEE ADVANCED ARCHIVE LEVEL 2 (TRUE FALSE TYPE)
Explore 4 Videos
Similar Questions
Knowledge Check
The length of a simple pendulum is made one-fourth. Its time period becomes :
Afour timesBone-fourthCdoubleDhalf
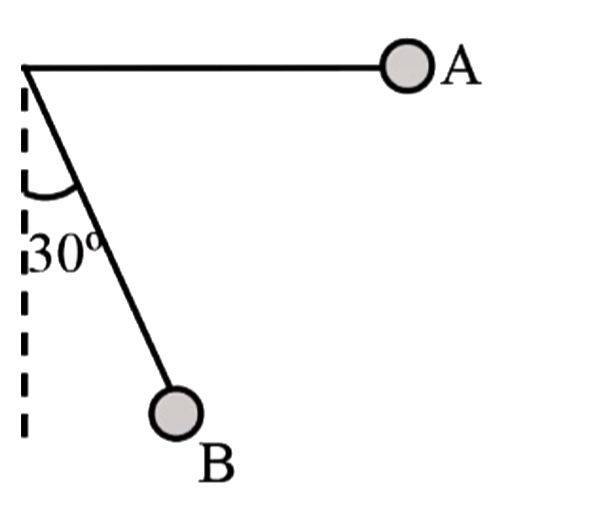
A simple pendulum is released from A as shown. If m and 1 represent the mass of the bob and length of the pendulum, the gain kinetic energy at B is
View SolutionThe time period Of oscillation of a simple pendulum depends on the following quantities
Length of the pendulum (l),
Mass of the bob (m), and
Acceleration due to gravity (g)
Derive an expression for Using dimensional method.
View SolutionThe period of a simple pendulum on the surface of the earth is 2s. Find its period on the surface of this moon, if the acceleration due to gravity on the moon is one-sixth that on the earth ?
View SolutionThe period of oscillation of a simple pendulum is given by T=2π√Lg, where L is the length of the pendulum and g is the acceleration due to gravity. The length is measured using a meter scale which has 500 divisions. If the measured value L is 50 cm, the accuracy in the determination of g is 1.1% and the time taken for 100 oscillations is 100 seconds, what should be the possible error in measurement of the clock in one minute (in milliseconds) ?
View SolutionState how does the time period of a simple pendulum depend on acceleration due to gravity.
View SolutionDoes the time period depend upon the mass, the size and the material of the bob.
View SolutionState how does the time period of a simple pendulum depend on mass of bob.
View Solution

