State how does the time period of a simple pendulum depend on acceleration due to gravity.
To determine how the time period of a simple pendulum depends on the acceleration due to gravity, we can follow these steps:
1. Understanding the Pendulum:
A simple pendulum consists of a mass (bob) attached to a string of length L that swings back and forth under the influence of gravity.
2. Restoring Force:
The restoring force acting on the pendulum is proportional to the displacement from its equilibrium position. For small angles, we can use the approximation sin(θ)≈θ (in radians). The restoring force F can be expressed as:
F=−mgsin(θ)≈−mgθ
where m is the mass of the bob and g is the acceleration due to gravity.
3. Displacement Relation:
The displacement s of the pendulum is related to the angle θ by the arc length formula:
s=Lθ
Thus, we can express θ as:
θ=sL
4. Form of the Restoring Force:
Substituting θ into the expression for the restoring force gives:
F=−mg(sL)=−mgLs
This shows that the restoring force is proportional to the displacement s, indicating simple harmonic motion.
5. Force Constant:
We can identify the force constant k as:
k=mgL
6. Time Period Formula:
The time period T of a simple harmonic oscillator is given by:
T=2π√mk
Substituting the expression for k:
T=2π√mmgL
Simplifying this gives:
T=2π√Lg
7. Conclusion:
From the final equation T=2π√Lg, we can see that the time period T of a simple pendulum depends on the length L of the pendulum and inversely on the square root of the acceleration due to gravity g. Therefore, as g increases, the time period T decreases, indicating that the pendulum swings faster.
A simple pendulum consists of a mass (bob) attached to a string of length L that swings back and forth under the influence of gravity.
The restoring force acting on the pendulum is proportional to the displacement from its equilibrium position. For small angles, we can use the approximation sin(θ)≈θ (in radians). The restoring force F can be expressed as:
F=−mgsin(θ)≈−mgθ
where m is the mass of the bob and g is the acceleration due to gravity.
The displacement s of the pendulum is related to the angle θ by the arc length formula:
s=Lθ
Thus, we can express θ as:
θ=sL
Substituting θ into the expression for the restoring force gives:
F=−mg(sL)=−mgLs
This shows that the restoring force is proportional to the displacement s, indicating simple harmonic motion.
We can identify the force constant k as:
k=mgL
The time period T of a simple harmonic oscillator is given by:
T=2π√mk
Substituting the expression for k:
T=2π√mmgL
Simplifying this gives:
T=2π√Lg
From the final equation T=2π√Lg, we can see that the time period T of a simple pendulum depends on the length L of the pendulum and inversely on the square root of the acceleration due to gravity g. Therefore, as g increases, the time period T decreases, indicating that the pendulum swings faster.
Topper's Solved these Questions
- MEASUREMENTS AND EXPERIMENTATION Book:ICSEChapter:MEASUREMENTS AND EXPERIMENTATION Exercise:TOPIC 2 SIMPLE PENDULUM (3 Marks Questions )
Explore 10 Videos
- MEASUREMENTS AND EXPERIMENTATION Book:ICSEChapter:MEASUREMENTS AND EXPERIMENTATION Exercise:TOPIC 2 SIMPLE PENDULUM (4 Marks Questions )
Explore 1 Video
- MEASUREMENTS AND EXPERIMENTATION Book:ICSEChapter:MEASUREMENTS AND EXPERIMENTATION Exercise:TOPIC 1 INTERNATIONAL SYSTEM OF UNITS (4 Marks Questions )
Explore 2 Videos
- MAGNETISM Book:ICSEChapter:MAGNETISM Exercise:EXERCISE-10(B) (Multiple Choice Type)
Explore 2 Videos
- MOTION IN ONE DIMENSION Book:ICSEChapter:MOTION IN ONE DIMENSION Exercise:EXERCISE -2 (C) ( Multiple choice type :)
Explore 17 Videos
Similar Questions
State how does the time period of a simple pendulum depend on mass of bob.
View SolutionState how does the time period of a simple pendulum depend on length of pendulum.
View SolutionState how does the time period of a simple pendulum depend on amplitude of oscillation .
View SolutionOn what factors does the period of a simple pendulum depend ?
View SolutionThe value of acceleration due to gravity
View SolutionCalculate the time period of a simple pendulum of length one meter. The acceleration due to gravity at the place is π2ms−2.
View Solution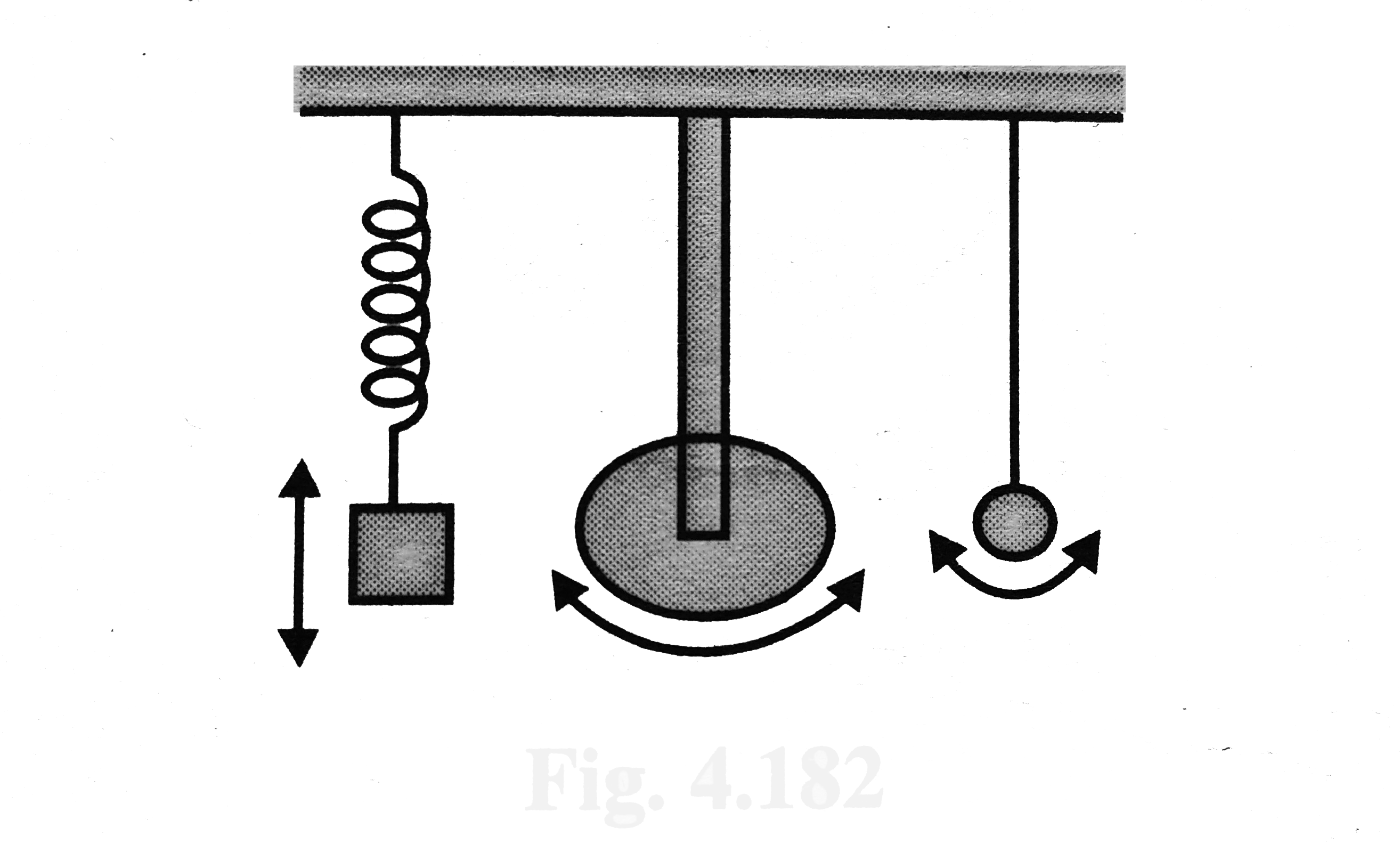
Q. Statement I Three pendulums are suspended from ceiling as shown in Fig. These three pendulums are set to oscillate as shon by arrows, and it is found that all three have same time period. Noe, all three are taken to a place where acceleration due to gravity changes to 4/9th of its value at the first place. If spring pendulum makes 60 cycles in a given time at this place, then torsion pendulum and simple pendulum will also make 60 oscillation in same (given) time interval. Statement II: Time period of torsion pendulum is independent of acceleration due to gravity.
View SolutionWhich of the following depends on acceleration due to gravity ?
View SolutionUsing dimensional analysis check the correctness of the equation T=2π√lg, where T is the period of the simple pendulum of length l and g is the acceleration due to gravity.
View SolutionThe time period of a simple pendulum of length 9.8 m is
View Solution