The magnetic field due to a conductor fo unifrom cross section of radius a and carrying a steady current is represented by
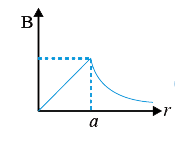
The correct Answer is:A
To solve the problem of finding the magnetic field due to a conductor of uniform cross-section of radius a carrying a steady current I, we can follow these steps:
Step 1: Understand the Geometry
We have a cylindrical conductor with radius a carrying a steady current I. We need to analyze the magnetic field both inside and outside the conductor.
Step 2: Apply Ampere's Law
We will use Ampere's Law, which states that:
∮B⋅dL=μ0Ienc
where Ienc is the current enclosed by the path of integration.
Step 3: Consider Inside the Conductor (r<a)
For points inside the conductor (where r is the distance from the center and r<a):
- The current density J is uniform, given by:
J=Iπa2
- The enclosed current Ienc for a radius r is:
Ienc=J⋅Area=J⋅πr2=Iπa2⋅πr2=Ir2a2
- Applying Ampere's Law:
B⋅(2πr)=μ0Ienc=μ0(Ir2a2)
- Thus,
B=μ0Ir2πa2
This shows that the magnetic field B inside the conductor is directly proportional to r.
Step 4: Consider Outside the Conductor (r≥a)
For points outside the conductor:
- The total current enclosed is simply I.
- Applying Ampere's Law:
B⋅(2πr)=μ0I
- Thus,
B=μ0I2πr
This shows that the magnetic field B outside the conductor is inversely proportional to r.
Step 5: Conclusion
From our analysis:
- Inside the conductor (r<a), B increases linearly with r.
- Outside the conductor (r≥a), B decreases inversely with r.
Step 6: Identify the Correct Representation
Given the options, the correct representation of the magnetic field as a function of distance from the center of the conductor will show a linear increase up to r=a and then a hyperbolic decrease for r>a. Thus, the correct option is A.
---
We have a cylindrical conductor with radius a carrying a steady current I. We need to analyze the magnetic field both inside and outside the conductor.
We will use Ampere's Law, which states that:
∮B⋅dL=μ0Ienc
where Ienc is the current enclosed by the path of integration.
For points inside the conductor (where r is the distance from the center and r<a):
- The current density J is uniform, given by:
J=Iπa2
- The enclosed current Ienc for a radius r is:
Ienc=J⋅Area=J⋅πr2=Iπa2⋅πr2=Ir2a2
- Applying Ampere's Law:
B⋅(2πr)=μ0Ienc=μ0(Ir2a2)
- Thus,
B=μ0Ir2πa2
This shows that the magnetic field B inside the conductor is directly proportional to r.
For points outside the conductor:
- The total current enclosed is simply I.
- Applying Ampere's Law:
B⋅(2πr)=μ0I
- Thus,
B=μ0I2πr
This shows that the magnetic field B outside the conductor is inversely proportional to r.
From our analysis:
- Inside the conductor (r<a), B increases linearly with r.
- Outside the conductor (r≥a), B decreases inversely with r.
Given the options, the correct representation of the magnetic field as a function of distance from the center of the conductor will show a linear increase up to r=a and then a hyperbolic decrease for r>a. Thus, the correct option is A.
Topper's Solved these Questions
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:ENABLE
Explore 50 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:EFFICIENT
Explore 50 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:MCQ
Explore 2 Videos
- PROPERTIES OF MATTERBook:VMC MODULES ENGLISHChapter:PROPERTIES OF MATTERExercise:JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
Explore 1 Video
Similar Questions
Find the magnetic field B due to a semicircular wire of radius 10.0 cm carrying a current of 5.0A at its centre of curvature .
View SolutionA long straight wire of a circular cross section (radius a) carrying steady current. Current is uniformly distributed in the wire. Calculate magnetic field inside the region (r<a) in the wire.
View SolutionA long straight wire of a circular cross-section of radius 'a' carries a steady current I. The current is uniformly distributed across the cross-section. Apply Ampere's circuital law to calculate the magnetic field at a point at distance 'r' in the region for (i) r<a and (ii) r>a.
View SolutionA long straight wire of a curcular cross-section of radius 'a' carries a steady current 'l'. The current is uniformly distributed the across- section . Apply Amphere's circuital law to calculate the magnetic field at a point 'r' in the region for (i) r<a and (ii) r>a.
View SolutionA wire of radius R having uniform cross section in which steady current l is flowing. Then
View SolutionThe magnetic field ¯¯¯¯¯dB due to a small current element ¯¯¯dl at a distance →r and carrying current 'I' is
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionFigure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

View SolutionThe magnetic field in a straight current carrying conductor wire is:
View SolutionA long cylinder of uniform cross section and radius R is carrying a current i along its length and current density is uniform cross section and radius r in the cylinder parallel to its length. The axis of the cylinderical cavity is separated by a distance d from the axis of the cylinder. Find the magnetic field at the axis of cylinder.
View Solution

