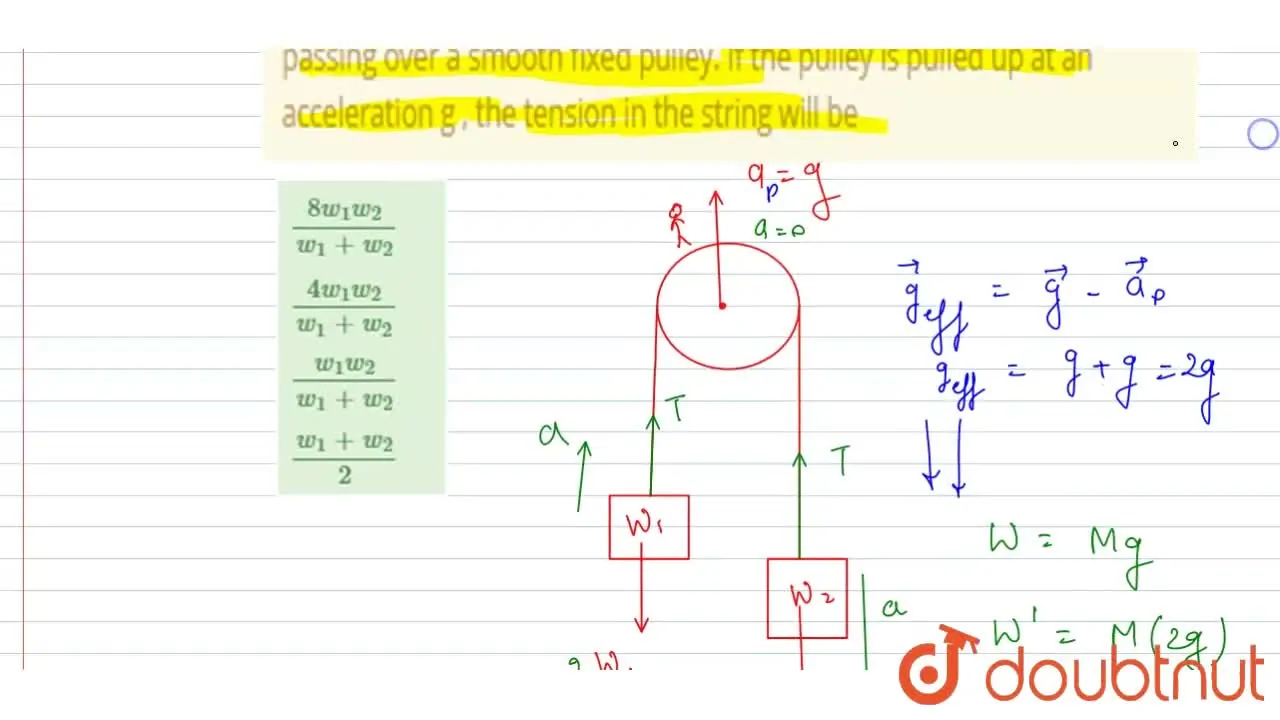
Two weights w1 and w2 are suspended from the ends of a light string passing over a smooth fixed pulley. If the pulley is pulled up at an acceleration g , the tension in the string will be
8w1w2w1+w2
4w1w2w1+w2
w1w2w1+w2
w1+w22
The correct Answer is:1
Step by step video & image solution for Two weights w_(1) and w_(2) are suspended from the ends of a light string passing over a smooth fixed pulley. If the pulley is pulled up at an acceleration g , the tension in the string will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE53videos
LAWS OF MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - ENABLE50videos
LAWS OF MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)14videos
KINEMATICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)55videos
LIQUIDS
Similar Questions
The weights W and 2W are suspended from the ends of a light string passing over a smooth fixed pulley. If the pulley is pulled up with an acceleration of 10m/s2, the tension in the string will be (g=10m/s2)
View SolutionTwo bodies of masses m1 and m2 are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration g2, then tension in the string will be
View SolutionTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
View SolutionTwo masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)
 View Solution
View SolutionTwo masses m and M(>m) are joined by a light string passing over a smooth light pulley. The centre of mass of the system moves with an acceleration
 View Solution
View SolutionThree weights are hanging over a smooth fixed pulley as shown in the figure. What is the tension in the string connecting weights B and C ?
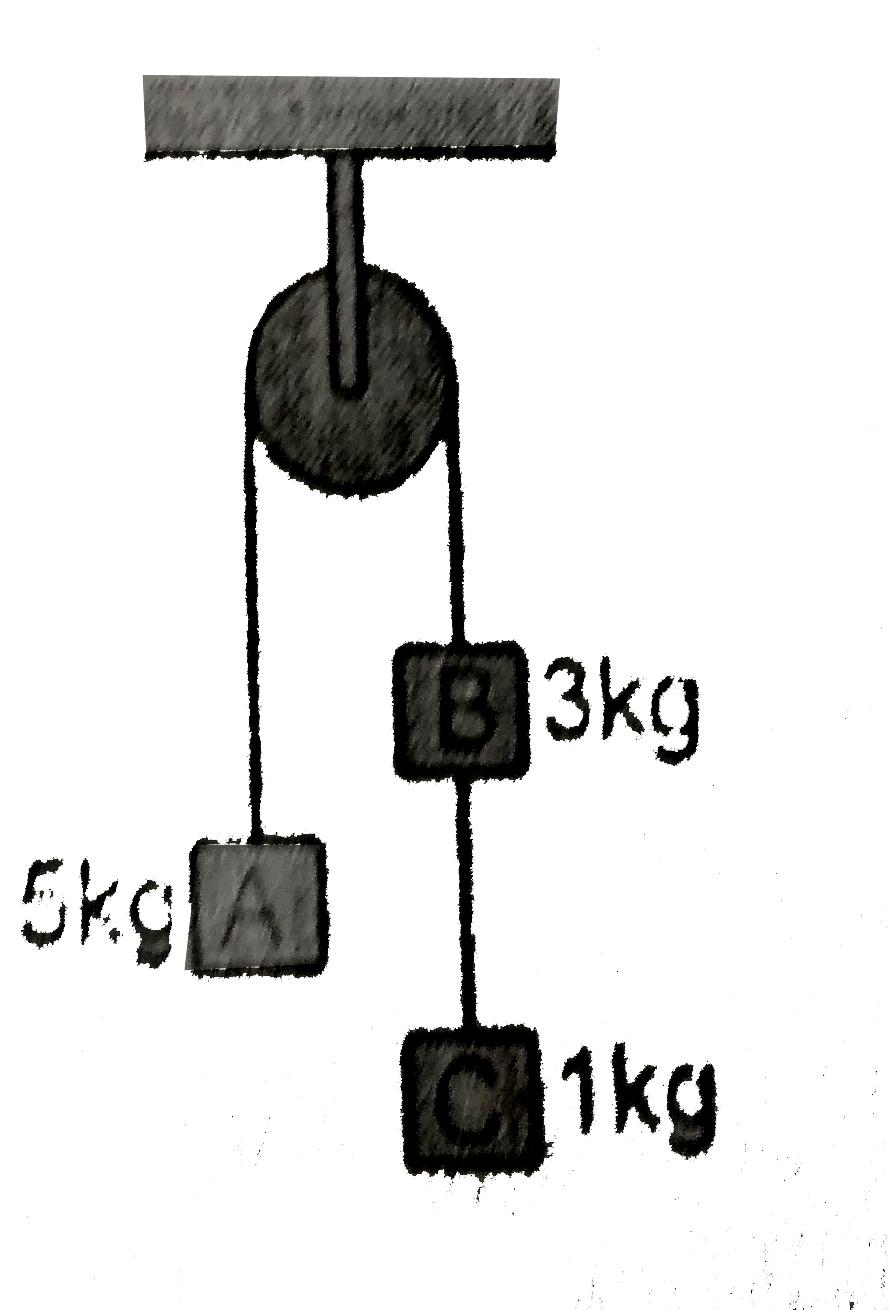 View Solution
View SolutionTwo masses m1andm2 are connected to the end of a string passing over a smooth pulley . The magnitude of tension in the string is T and the masses are moving with magnitude of acceleration a . If the masses are interchanged , then
View SolutionTwo masses 8 kg and 12 kg are connected at the two ends of a light in extensible string that passes over a friction less pulley Find the acceleration of the masses and tension in the string , when the masses are released
 . View Solution
. View Solutiontwo masses 2m and m are attached to the the ends of a string while passing over a smooth Pulley of mass m and radius R. The ratio of tensions in both the strings is
_PHY_E05_245_Q01.png) View Solution
View SolutionTwo bodies of masses 1 kg and 2 kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string
View Solution