How much time is requred for two - third completion of a first order reaction having, K=5.48×10−14S−1?
2.01×1011s
2.01×1013s
8.08×1013s
16.04×1011 s
The correct Answer is:B
To solve the problem of finding the time required for two-thirds completion of a first-order reaction with a rate constant K=5.48×10−14s−1, we can follow these steps:
Step 1: Understand the Reaction Completion
For a first-order reaction, if two-thirds of the reactant has reacted, it means that one-third of the reactant remains. If we denote the initial concentration as A0, then after two-thirds completion, the remaining concentration A is:
A=A0−23A0=13A0
Step 2: Use the First-Order Kinetics Formula
The integrated rate law for a first-order reaction is given by:
t=1kln(A0A)
Substituting A=13A0 into the equation gives:
t=1kln⎛⎝A013A0⎞⎠
Step 3: Simplify the Equation
This simplifies to:
t=1kln(3)
Step 4: Substitute the Value of k
Now, substituting the given value of k:
t=15.48×10−14ln(3)
Step 5: Calculate ln(3)
The natural logarithm of 3 is approximately:
ln(3)≈1.0986
Step 6: Calculate the Time
Now substituting ln(3) back into the equation:
t=1.09865.48×10−14
Step 7: Perform the Calculation
Calculating the above expression:
t≈2.00×1013s
Final Answer
Thus, the time required for two-thirds completion of the reaction is approximately:
t≈2.00×1013s
For a first-order reaction, if two-thirds of the reactant has reacted, it means that one-third of the reactant remains. If we denote the initial concentration as A0, then after two-thirds completion, the remaining concentration A is:
A=A0−23A0=13A0
The integrated rate law for a first-order reaction is given by:
t=1kln(A0A)
Substituting A=13A0 into the equation gives:
t=1kln⎛⎝A013A0⎞⎠
This simplifies to:
t=1kln(3)
Now, substituting the given value of k:
t=15.48×10−14ln(3)
The natural logarithm of 3 is approximately:
ln(3)≈1.0986
Now substituting ln(3) back into the equation:
t=1.09865.48×10−14
Calculating the above expression:
t≈2.00×1013s
Thus, the time required for two-thirds completion of the reaction is approximately:
t≈2.00×1013s
Topper's Solved these Questions
- CHEMICAL KINETICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL KINETICS EXERCISE - Level-2 ( Numerical Value Type for JEE Main )
15 Videos
- CHEMICAL KINETICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL KINETICS EXERCISE - JEE Main (Archive)
56 Videos
- CHEMICAL KINETICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL KINETICS EXERCISE - Level-1
75 Videos
- CHEMICAL EQUILIBRIUMBOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - IN-CHAPTER EXERCISE - G
10 Videos
- CHEMICAL THERMODYNAMICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL THERMODYNAMICS EXERCISE - IN - CHAPTER EXERCISE - L
10 Videos
Similar Questions
The half-life period of a first order reaction having rate constant k=0.231×10−10s−1 will be:
View Solution(a) For a reaction AB→P , the rate law is given by, r=k[A]1/2[B]2. What is the order of this reaction?
(b) A first order reaction is found to have a rate constant k=5.5×10−14s−1, Find the half life of the reaction.
View SolutionThe time required for 10% completion of a first order reaction at 298K is equal to that required for its 25% completion at 308K . If the value of A is 4×1010s−1, calculate k at 318K and Ea.
View SolutionThe substance undergoes first order decomposition. The decomposition follows two parallel first order reactions as :
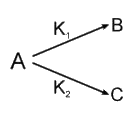
K1=1.26×10−4sec−1andK2=3.8×10−5sec−1 The percentage distribution of B and C
View SolutionA substance undergoes first order decomposition. The decomposition follows two parallel first order reaction as:
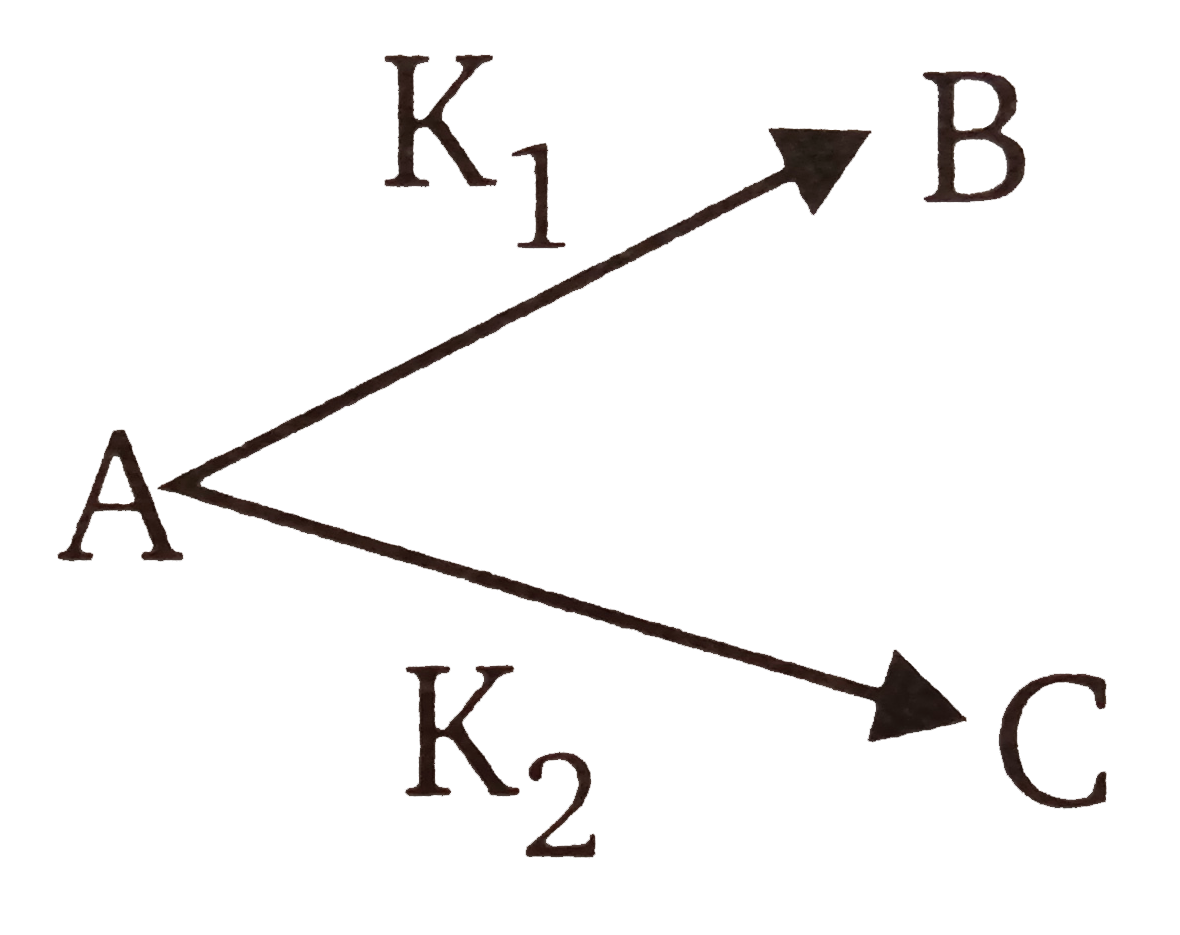 and KP1=1.26×10−4sec−1
and KP1=1.26×10−4sec−1
K2=3.80×10−5sec−1
The percentage distribution of B and C are:
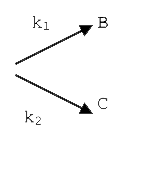
View SolutionA substance undergoes first order decomposition. The decomposition follows two parallel first order reactions as :
k1=1.26×10−4s−1,k2=3.8×10−5s−1
The percentage distribution of B and C are :
View SolutionAfter how many seconds will the concentration of the reactant in a first order reaction be halved if the rate constant is 1.155×10−3s−1?
View SolutionIf the rate constant for a second order reaction is 2.303×10−3s−1 then the time required for the completion of 70% of the reaction is (log3=0.48)
View SolutionIdentify the reaction order from each of the following rate :
k=3.1×10−4s−1
View SolutionIdentify the reaction order from each of the following rate :
k=3.1×10−4s−1
View Solution
