A spherical shell of radius R has a uniformly distributed charge ,then electric field varies as
The potential at the centre of the shells is reduced by 2αV0 .
The magnitude of electric field apoint located on a line passing through the hole and shell’s center, on a distance from the center of the spherical shell will be reduced by αV02R
The magnitude of electric field at the center of the shell is reduced by (αV0)(2R)
The ratio of the potential at the center of the cell to that of the point at 12R from centertowards the hole will be 1−α1−2α
The correct Answer is:D
(A) The potential is reduced by dv=kdqR
Also, v0=kQR∴dvv0=dqQ=(σα4πR2σ(4πR2)=α⇒dv=αv0
∴ A is wrong
(B) The field is reduced by dE=kdqR2=dvR=αv0R∴ B is wrong
(C) Initial field at centre is zero, so field increases by dE=kdqR2=dvR=αv0R∴ (C) is wrong
Potential at centre =v0−dv=(l−α)v0
Potential at R2=v0−kdq(R/2)=v0−2dv=(l−2α)v0∴ Ratio=1−α1−2α (D) is correct
Topper's Solved these Questions
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:JEE MAIN
Explore 65 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT Book:VMC MODULES ENGLISHChapter:ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT Exercise:IMPECCABLE
Explore 52 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
Explore 1 Video
Similar Questions
A spherical shell of radius R carries a uniformly distributed charge q. The electrical forces arising cause the ex-pansion of the shell. Find the mechanical stress in the shell.
View SolutionA charge Q is uniformly distributed in a dielectric sphere of radius R (having dielectric constant unity). This dielectric sphere is enclosed by a concentric spherical shell of radius 2R and having uniformly distributed charge 2Q. Which of the following graph correctly represents variation of electric field with distance r from the common centre?

View Solution
Knowledge Check
Consider a thin spherical shell of radius R consisting of uniform surface charge density σ. The electric field at a point of distance x from its centre and outside the shell is
Ainversely proportional to σBdirectly proportional to x2Cdirectlr proportional to RDinversely proportional to x2There is a solid sphere of radius R having uniformly distributed charge throughout it. What is the relation between electric field E and distance r from the centre (r is less than R) ?
AE∝r−2BE∝r−1CE∝rDE∝r2
A thin spherical shell radius of R has a charge Q uniformly distributed on it. At the centre of the shell, a negative point charge -q is placed. If the shell is cut into two identical hemispheres, still equilibrium is maintained. Then find the relation between Q and q?

View SolutionA spherical shell of radius R=1.5cm has a charge q=20μC uniformly distributed over it. The force exerted by one half over the other half is
View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
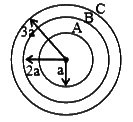
View SolutionThree concentric spherical shells A, B and C having uniformly distributed total charges +Q, -2Q and +Q respectively are placed as shown. The potential at the centre will be -
View SolutionA circular ring carries a uniformly distributed positive charge .The electric field(E) and potential (V) varies with distance (r ) from the centre of thr ring along its axis as

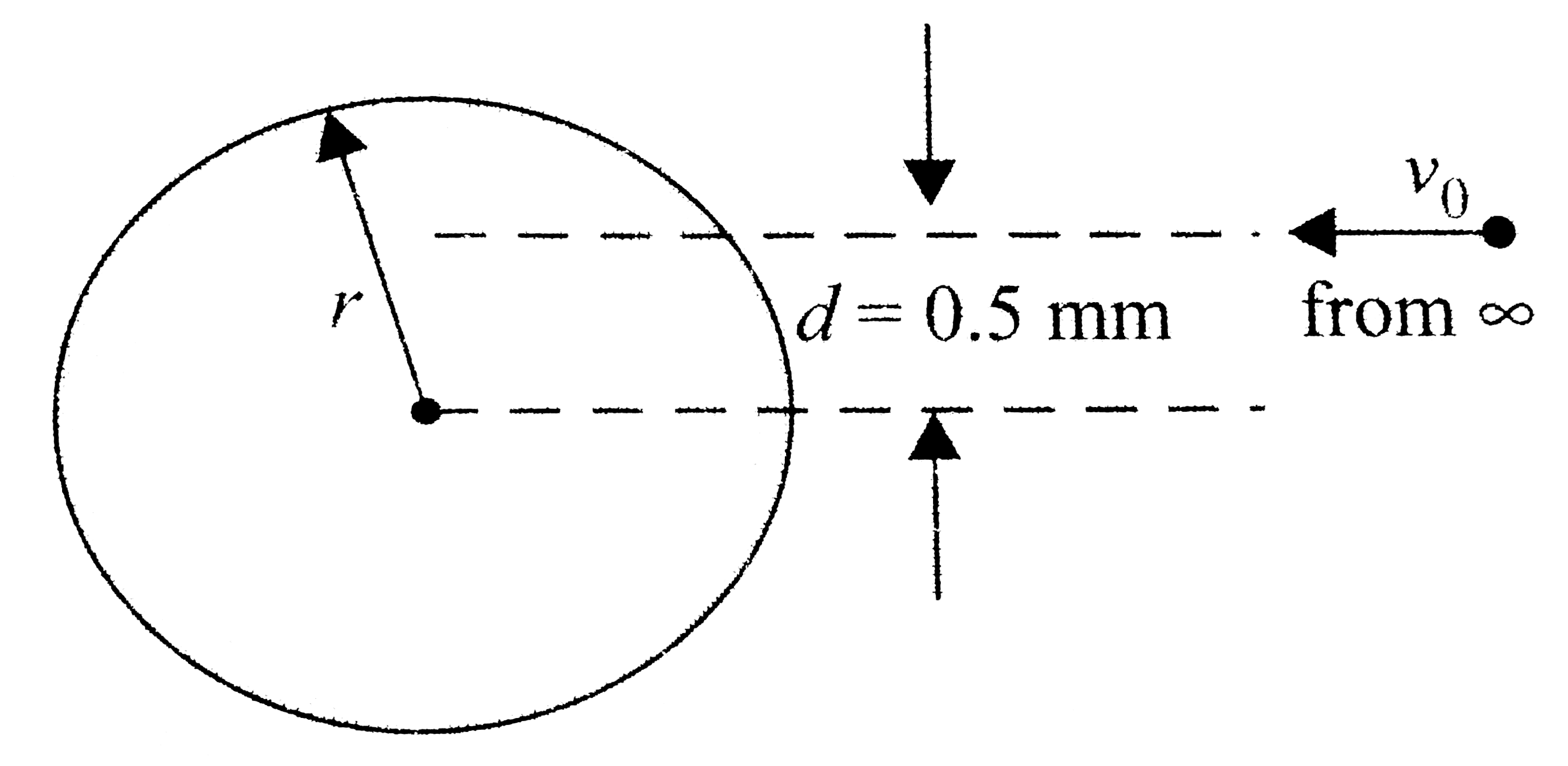
View SolutionA particle of mass 1kg and charge 1/3μC is projected toward a nonconducing fixed spherical shell of radius r=1mm having the same charge uniformly distributed on its surface. Find th minimum initial velocity of projection requires if the particle just grazes the shell.
 .
.
View Solution