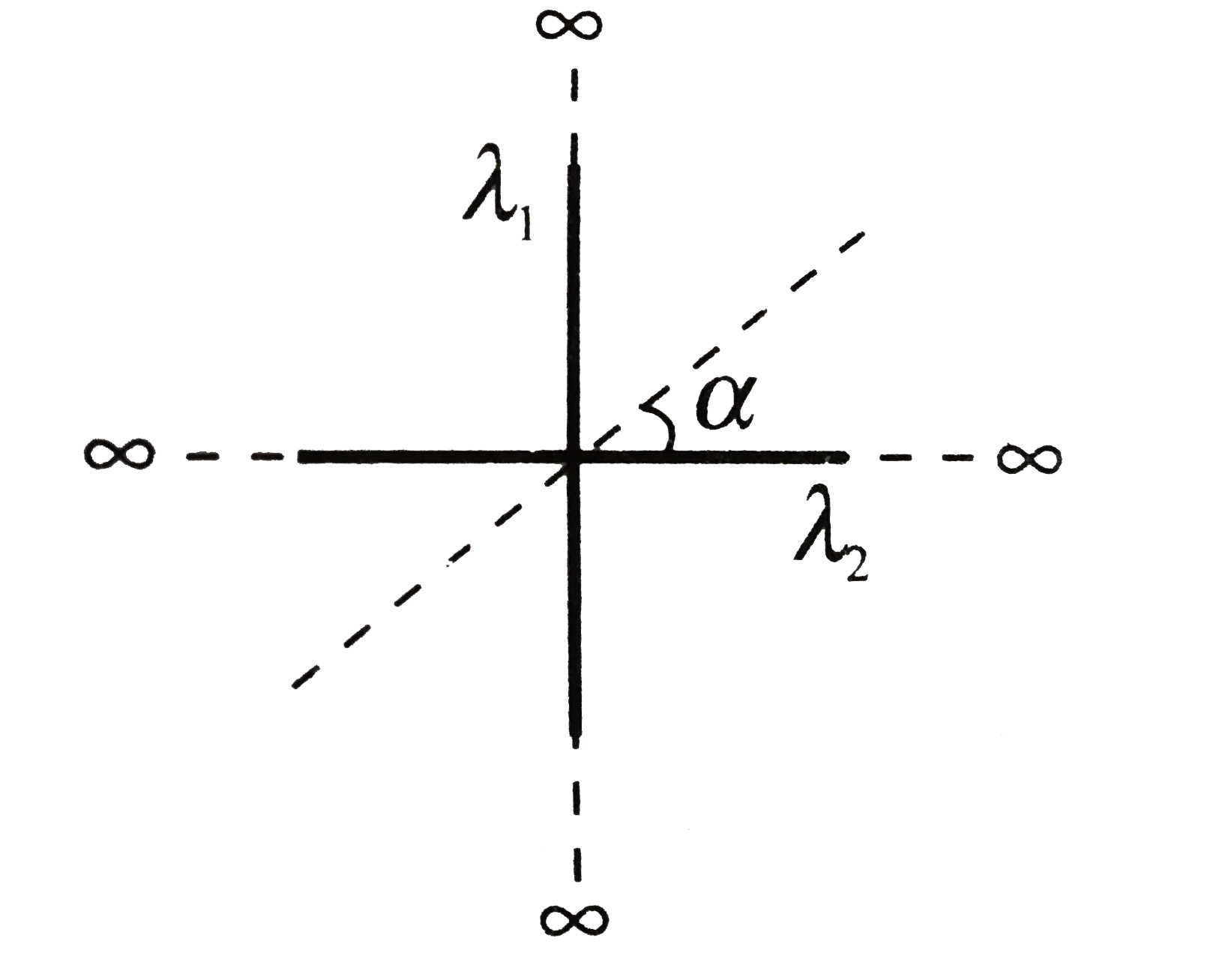
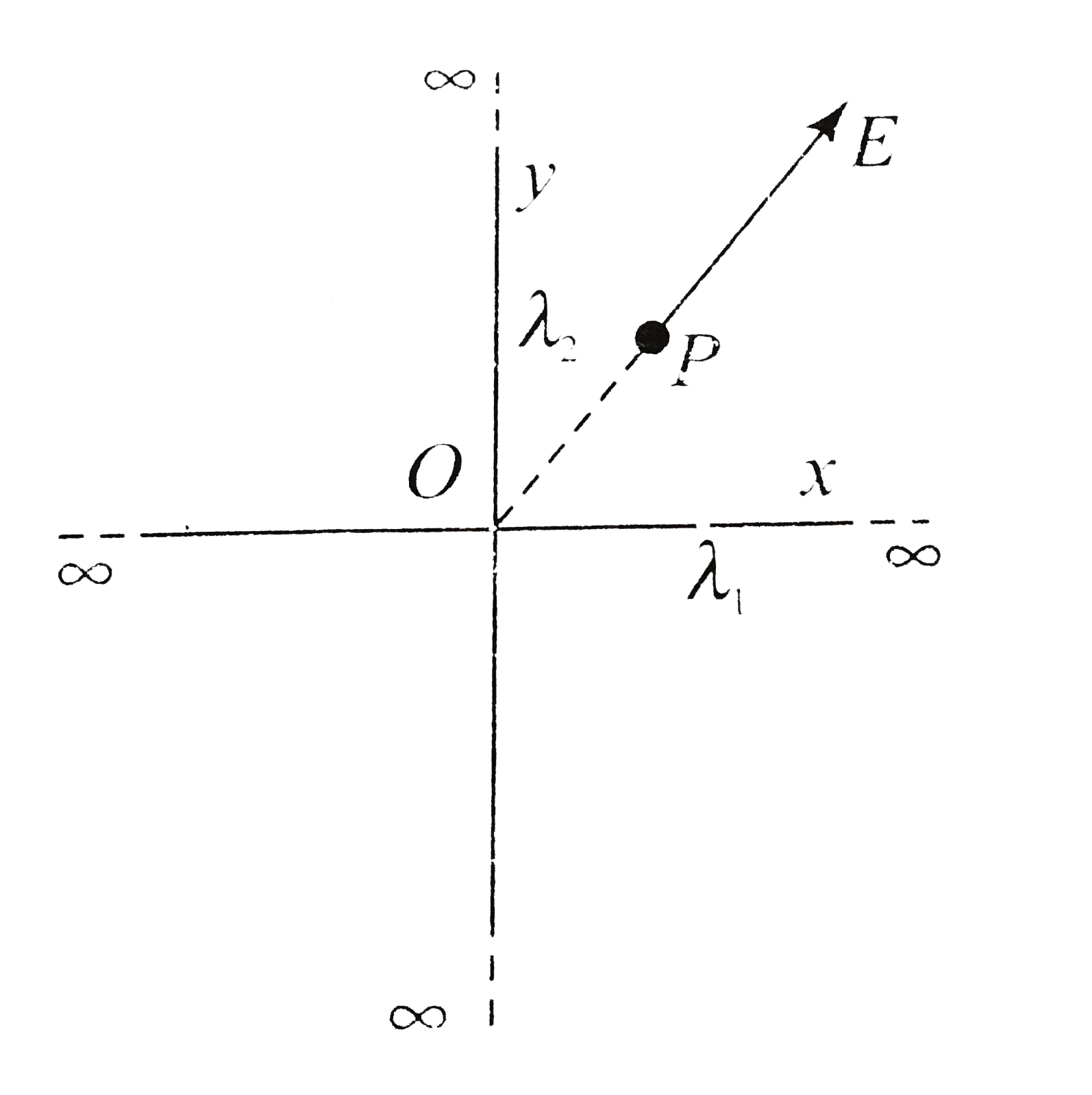
Two mutually perpendicular infinite wires along x-axis and y-axis carry charge densities λ1andλ2. The electric line of force at P is along the line y=x/(√3), where P is also a point lying on the same line. Find λ2/λ1.
The correct Answer is:C
Net electric field is ¯p,→E=→E1+→E2 due to vertical wire
→E2=λ22πe0x due to vertical wire in x-direction, a angle of electric field with x direction
tana=E1E2=λ1/2πe0yλ2/2πe0xor1√3=λ1xλ2yorλ2λ1=xy√3orλ2λ1=3
Topper's Solved these Questions
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:JEE MAIN
Explore 65 Videos
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:JEE Advanced (Archive)
Explore 89 Videos
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:LEVEL - 1
Explore 105 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT Book:VMC MODULES ENGLISHChapter:ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT Exercise:IMPECCABLE
Explore 52 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
Explore 1 Video
Similar Questions
Knowledge Check
The line xa−yb=1 cuts the x-axis at P. The equation of the line through P and perpendicular to the given line is
A(a) x+y=abB(b) x+y=a+bC(c) ax+by=a2D(d) bx+ay=b2
For an infinite line of charge having linear charge density λ lying along x-axis the work done in moving a charge q form C to A along CA is
View SolutionTwo uniformly long charged wires with linear densities λ and 3λ are placed along X and Y axis respectively. Determined the slope of electric field at any point on the l ine y=√3x
View SolutionAn infinite thread of charge density λ lies along z-axis. The potential difference between points A(4,3,4) and (3,4,0) is
View SolutionTwo particle are moving perpendicular to each with de-Broglie wave length λ1 and λ2. If they collide and stick then the de-Broglie wave length of system after collision is : (A) λ=λ1λ2√λ21+λ22 (B) λ=λ1√λ21+λ22 (C) λ=√λ21+λ22λ2 (D) λ=λ1λ2√λ1+λ2
View Solution(i) Two infinitely long line charges each of linear charge density λ are placed at an angle θ as shown in figure. Find out electric field intensity at a point P, which is at a distance x from point O along angle bisector of line charges.
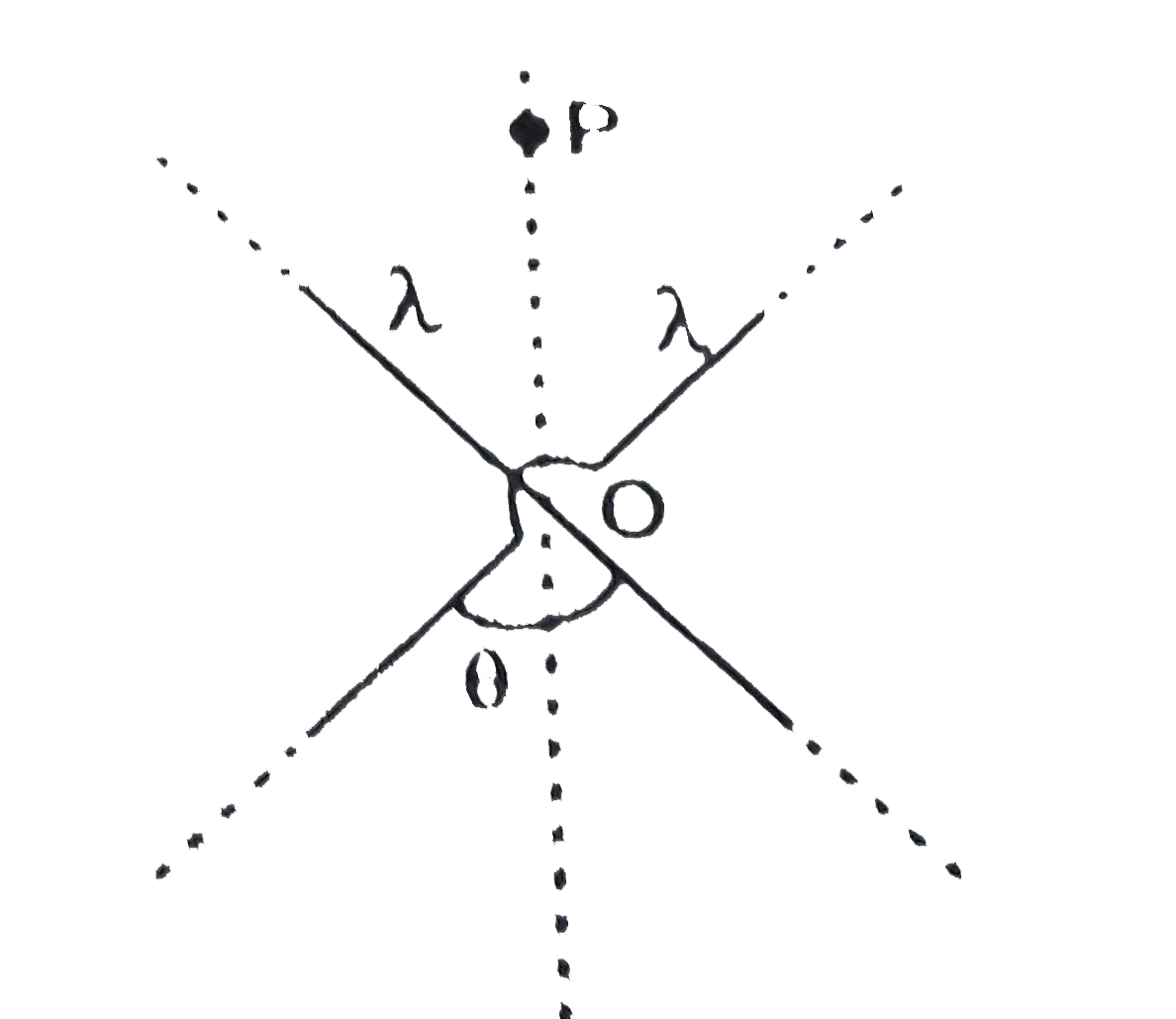
(ii) Repeat the above question if the line charge densities are λ and −λ. as shown in figure.

View SolutionLength of the shortest chord of the parabola y2=4x+8, which belongs to the family of lines (1+λ)y+(λ−1)x+2(1−λ)=0 is
View SolutionConsider the family of lines 5x+3y−2+λ1(3x−y−4)=0 and x−y+1+λ2(2x−y−2)=0. Find the equation of a straight line that belongs to both the families.
View Solution