The moment of inertia of a door of mass m, length 2l and width l about its longer side is
11mI224
5mI224
mI23
None of these
The correct Answer is:C
(about (YY')) =mI212
Using parallel axis theorem,
I(about AD) = mI212+mI24=mI23

Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 1 (Angular Momentum, Collision)
15 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 1 (Mixed topics)
15 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL-0 (LA: Long Answer Type)
3 Videos
- REVISION TEST-2 JEEBOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS
25 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
Similar Questions
The moment of inertia of a door of mass m, length 2l and width l about its longer side is.
View SolutionThe moment of inertia of a uniform cylinder of length landradiusR about its perpendicular bisector is I. What is the ratio l/R such that the moment of inertia is minimum ?
View SolutionIn Fig. find moment of inertia of a plate having mass M, length l and width b about axes 1,2,3 and 4. Assume that C is the centre and mass is uniformly distributed.
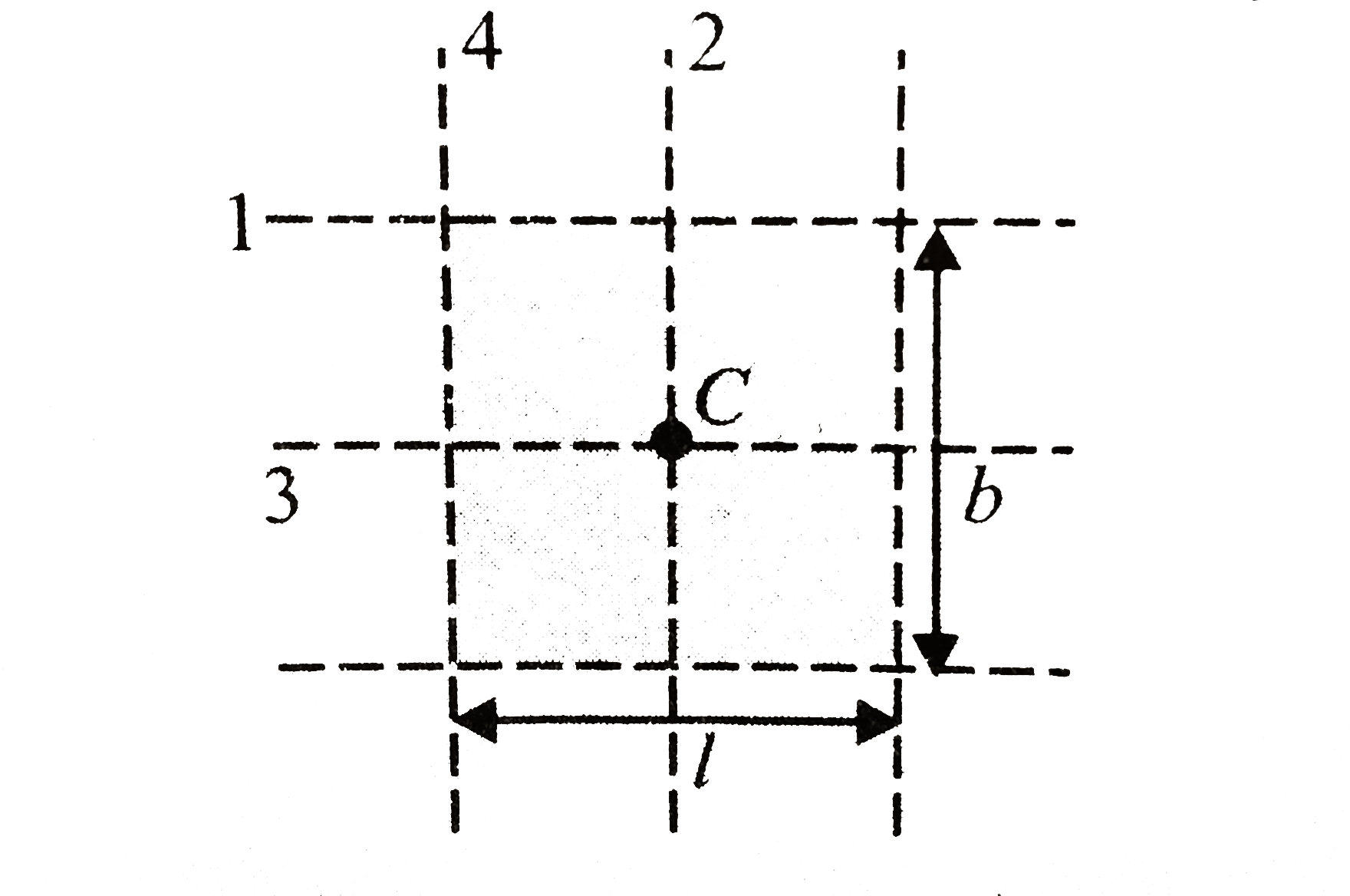
View SolutionThe moment of inertia of a system of four rods each of length l and mass m about the axis shown is
View SolutionMoment of inertia of a cylinder of mass M, length L and radius R about an axis passing through its centre and perpendicular to the axis of the cylinder is I=M(R24+L212). If such a cylinder is to be made for a given mass of a material, the ratio L/R for it to have minimum possible I is :
View SolutionThe moment of inertia of a cube of mass m and side a about one of its edges is equal to
View SolutionMoment of inertia of a rod of mass m and length l about its one end is I. If one-fourth of its length is cut away, then moment of inertia of the remaining rod about its one end will be
View SolutionCalculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
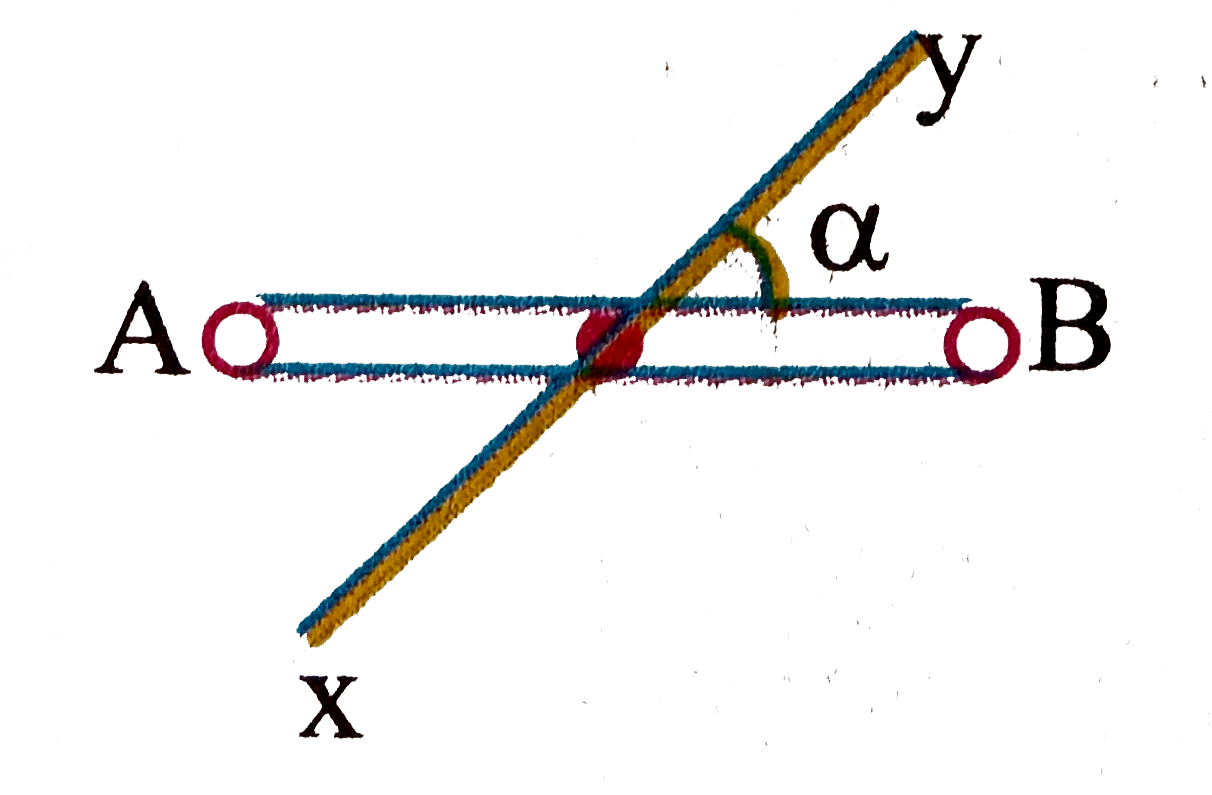
View SolutionThe moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an enable α is
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be

View Solution
