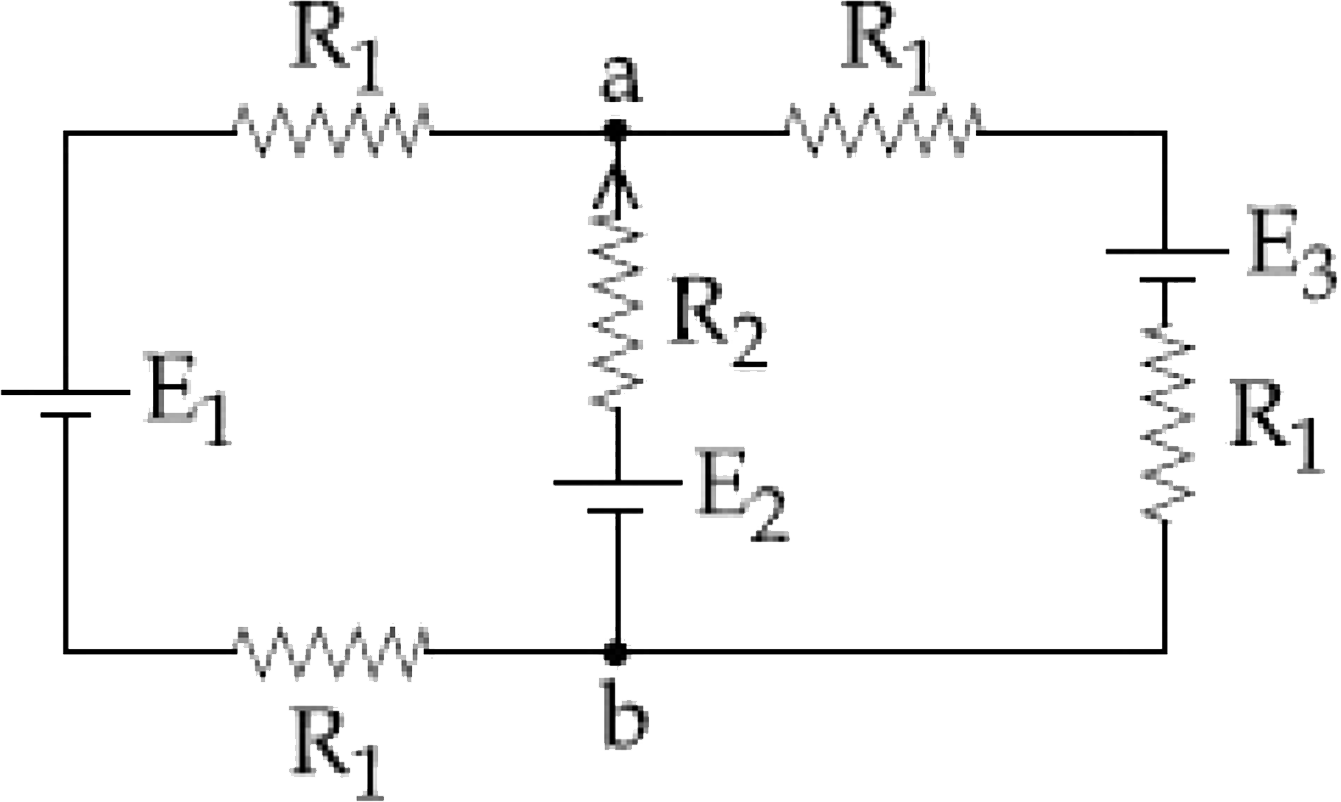
For the circuit shown, with and , the potential difference between the points and is approximately (in ):
3.7
2.7
3.3
2.3
Topper's Solved these Questions
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:JEE ADVANCED ARCHIVE
Explore 68 Videos
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:LEVEL-2 DAILY TUTORIAL SHEET-5
Explore 10 Videos
- CURRENT ELECTRICITYBook:VMC MODULES ENGLISHChapter:CURRENT ELECTRICITYExercise:IN-CHAPTER EXERCISE-F
Explore 10 Videos
- DYNAMICS OF A PARTICLEBook:VMC MODULES ENGLISHChapter:DYNAMICS OF A PARTICLEExercise:JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
Explore 31 Videos
Similar Questions
In the given network of ideal cells and resistors, R1=1.0Ω,R2=2.0Ω,E1=2V and E2=E3=4V. The potential difference between the point a and b is
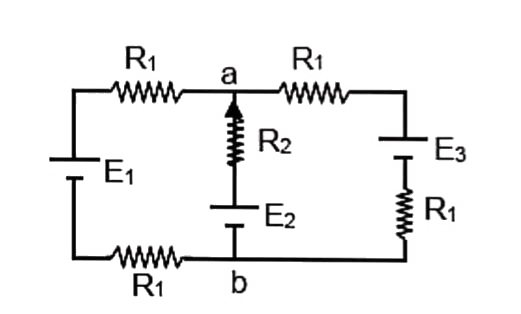
View SolutionCalculate the effective resistance between the points A and B in the circuit shown in Fig.
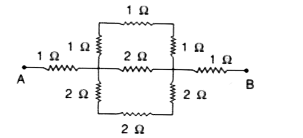
View SolutionPotential difference between points A and B (i.e. VA−VB) is -----
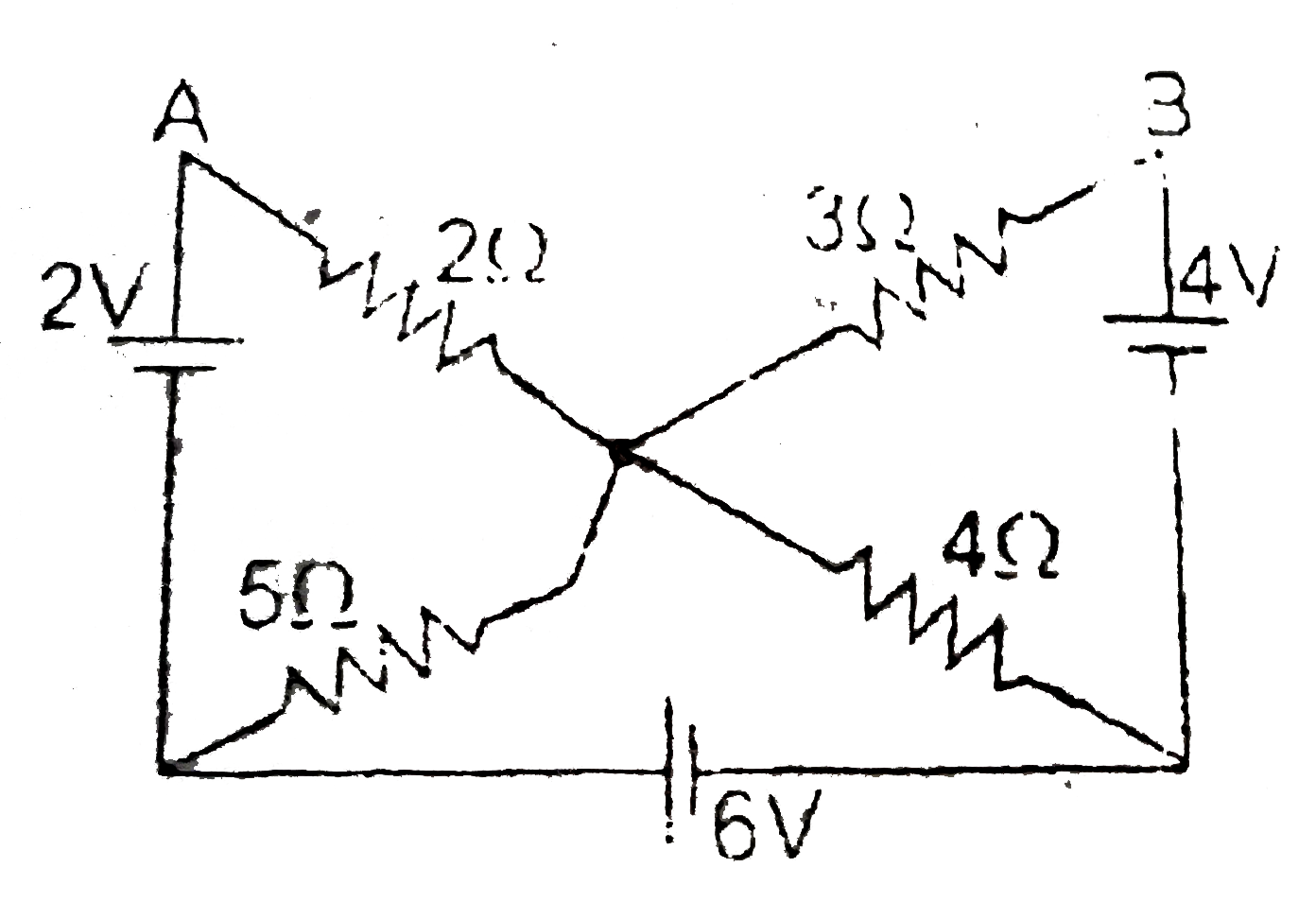
View SolutionIn the circuit shown in figure ,(ε)1=3V,(ε)2=2V,(ε)3=1Vandr1=r2=r3=1(Ω).Find the potential difference between the points A and B and the current through each branch.

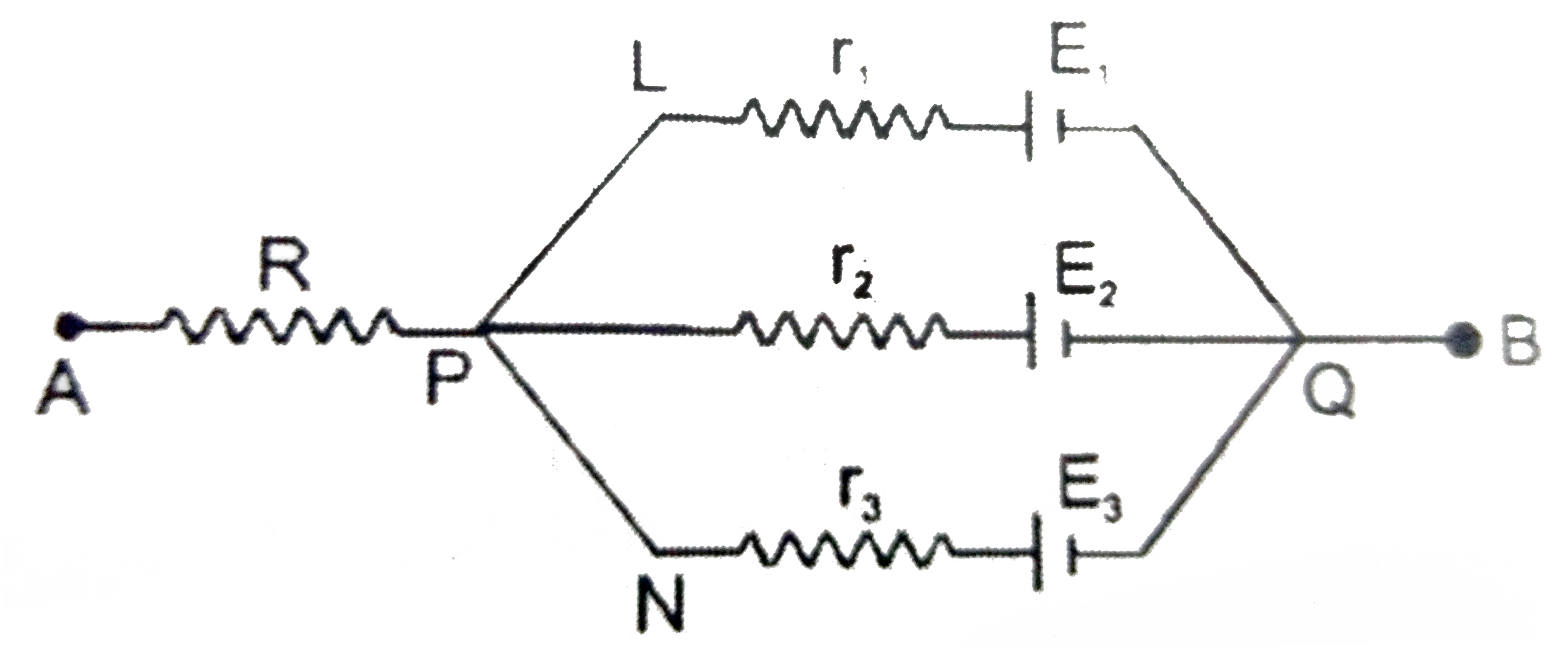
View SolutionIn the circuit shown in fig. E1=3 volt,E2=2 volt,E3=1 vole and R=r1=r2=r3=1ohm.
(i) Find potential difference in Volt between the points A and B with A & B unconnected.
(ii) If r2 is short circuited and the point A is coneted to point B through a zero resistance wire, find the current through R in ampere.
View SolutionIn the circuit in figure E1=3V,E2=2V,E3=1V and R=r1=r2=r3=1Ω
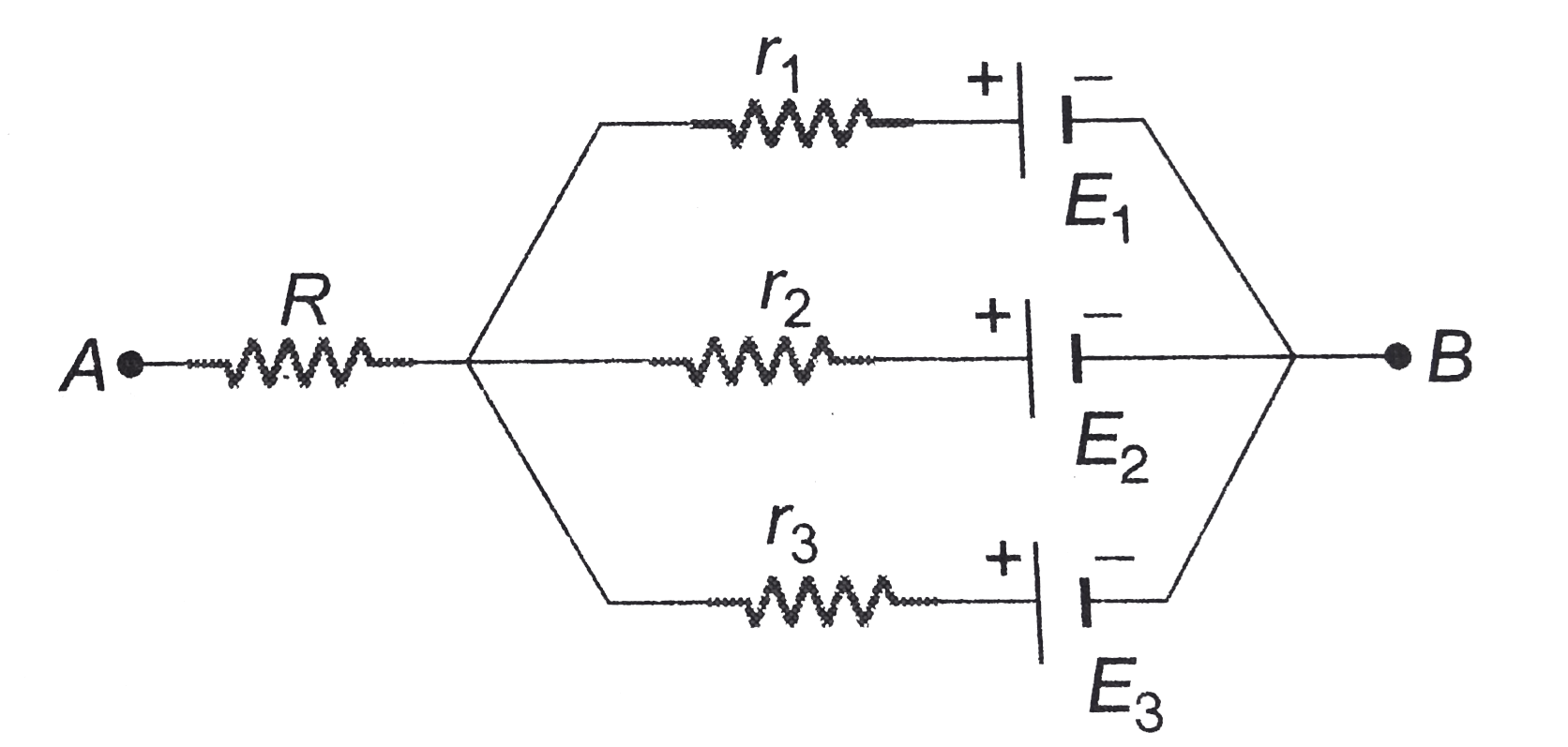
Find the potential differece between the points A and B and the currents through each branch.
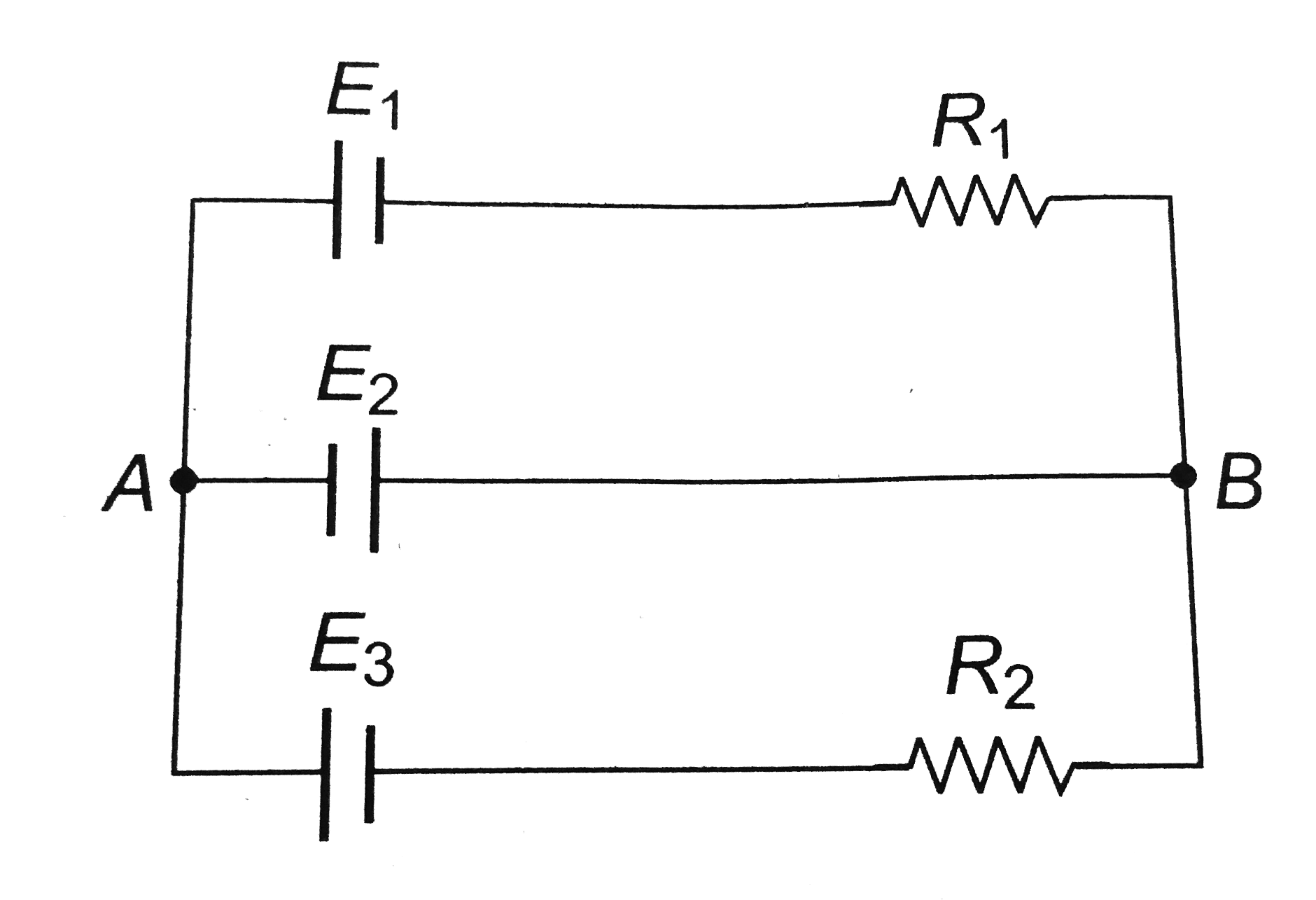
View SolutionIn the circuit shown here, E1=E2=E3=2V and R1=R2=4ohms. The current flowing between point A and B through battery E2 is
View SolutionIn the given circuit, R1 = 10Ω R2=6Ω and E = 10V, then correct statement is
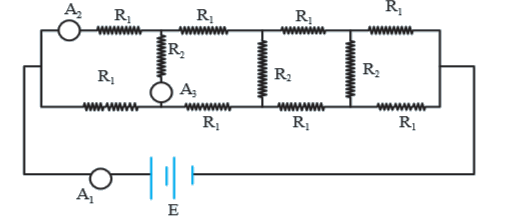
View SolutionIn the circuit shown below E1=4.0V,R1=2Ω,E2=6.0V,R2=4Ω and R3=2Ω. The current I1 is
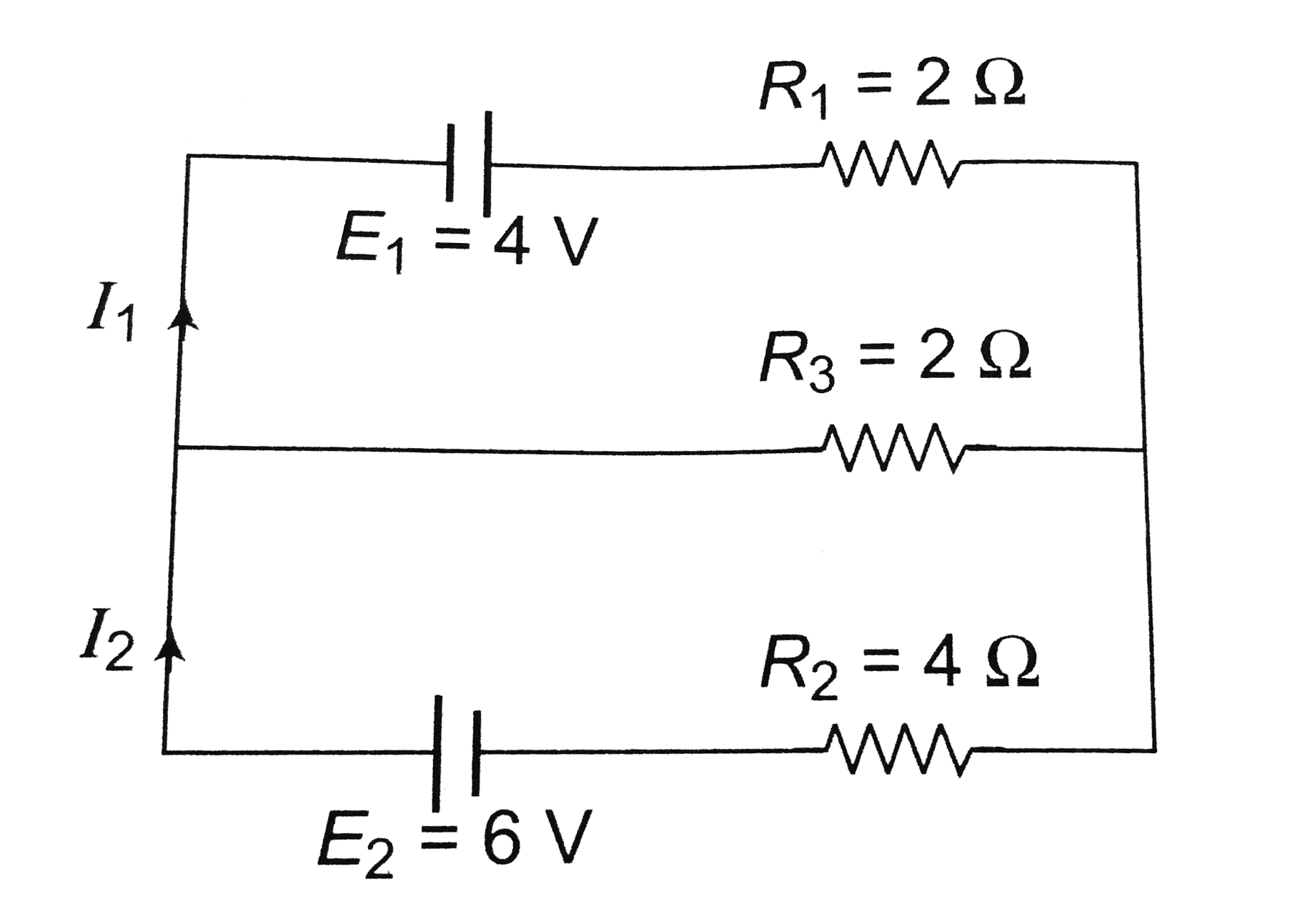
View SolutionIn the circuit shown in figure
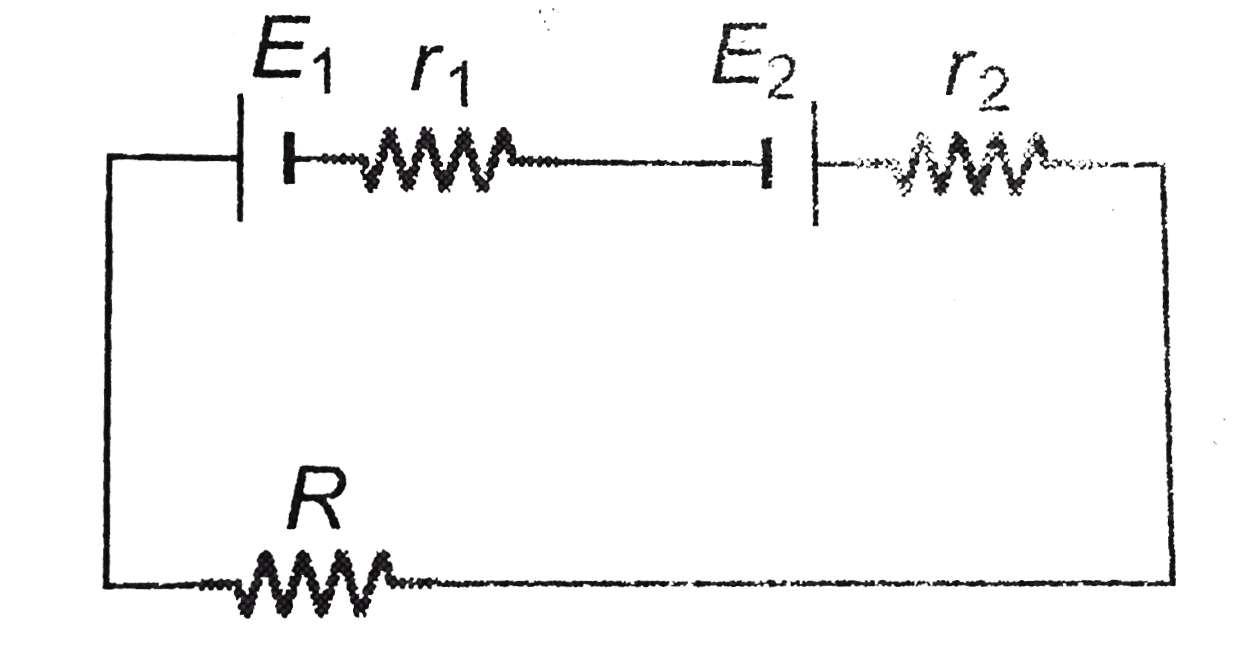
E1=10V,E2=4V,r1=r2=1Ω and R=2Ω.
Find the potential difference across battery 1 and battery 2.
View Solution