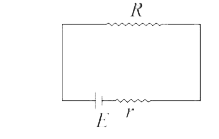
A cell of internal resistance r drivers current through an external resistance R. The power delivered by the to the external resistance will be maximum when:
R=0.001r
R=1000r
R=2r
R=r
i=ER+r,P=i2R=E2R(R+r)2
For maximum power , dPdR=0⇒R=r
Topper's Solved these Questions
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE
68 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-5
10 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
Similar Questions
A cell of e.m.f. E and internal resistance r is used to send current to an external resistance R. Write expressions for (a) the total resistance of circuit, (b) the current drawn from the cell, (c) the p.d. across the cell, and (d) voltage drop inside the cell.
View SolutionA cell of emf E and internal resistance r is connected in series with an external resistance nr. Than what will be the ratio of the terminal potential difference to emf, if n=9.
View Solution
Knowledge Check
In a circuit a cell with internal resistance r is connected to an external resistance R. The condition for the maximum current that drawn from the cell is
AR=rBR<rCR>rDR=0
A cell of e.m.f E and internal resitance r ,is connected to an external resistance R. the variation of potential difference V across the resistance R as function of R as shown in the figure, is the best represented by curve
_PHY_E01_011_Q01.png)
View SolutionTwo cells of 1.5 V and 2 V , having internal resistances of 1Ω and 2Ω respectively, are connected in parallel so as to read the current in the same direction through an external resistance of 5Ω . The current in the external resistance will be
View SolutionA battery is of emt E and internal resistance R. The value of external resistance r so that the power across eternal resistance is maximum :
View SolutionTwo cells , each of emfE and internal resistance r, are connected in parallel across a resistor R. The power delivered to the resistor is maximum if R is equal to
View SolutionA cell of emf ε and internal resistance r is connected across a load resistance R
(i) Find the maximum power delivered at the load ?
.
View SolutionConsider N=n1n2indentical cells, each of emf(ε) and internal resistance r. Suppose n1 cells are joined in series to forn a line and n_(2) such are connected in parallel. The combination drives a current in an external resistance R.(a) find the current in the external resistance, (b) Assuming that n1and n_(2) can be continuously varied, find the relation between n_(1) ,n_(2) R and r for which the current in R in maximum.
View SolutionA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
View Solution
