A constant potential difference is applied across a metal wire. Let the average thermal velocity of electrons in the wire be vt and let the drift velocity be vd . As the temperature of the wire rises:
Both vt and vd increase
Both vt and vd deccrease
vt increases and vd decreases
vt increases and vd decreases
To solve the problem, we need to analyze the behavior of both the average thermal velocity of electrons (v_t) and the drift velocity (v_d) in a metal wire as the temperature rises when a constant potential difference is applied.
1. Understanding Drift Velocity (v_d):
- The drift velocity (v_d) of electrons in a conductor is given by the formula:
vd=InqA
where I is the current, n is the number density of charge carriers, q is the charge of an electron, and A is the cross-sectional area of the wire.
- Drift velocity is also related to the relaxation time (τ) by the equation:
vd∝τ
2. Effect of Temperature on Relaxation Time (τ):
- As the temperature of the metal wire increases, the thermal agitation of the lattice ions increases, leading to more frequent collisions between electrons and lattice ions.
- This results in a decrease in the relaxation time (τ), which is the average time between collisions of the electrons. Therefore, we can conclude:
As temperature increases, τ decreases.
3. Impact on Drift Velocity (v_d):
- Since drift velocity is directly proportional to relaxation time, if τ decreases, then:
vd decreases.
4. Understanding Average Thermal Velocity (v_t):
- The average thermal velocity (v_t) of electrons is related to their kinetic energy, which is influenced by temperature. As temperature increases, the kinetic energy of the electrons increases, leading to an increase in their average thermal velocity.
- Therefore, we can conclude:
As temperature increases, vt increases.
5. Final Summary:
- As the temperature of the wire rises:
- The drift velocity vd decreases due to the decrease in relaxation time.
- The average thermal velocity vt increases due to increased kinetic energy.
Conclusion:
- The correct answer is that as the temperature increases, the average thermal velocity vt increases while the drift velocity vd decreases.
- The drift velocity (v_d) of electrons in a conductor is given by the formula:
vd=InqA
where I is the current, n is the number density of charge carriers, q is the charge of an electron, and A is the cross-sectional area of the wire.
- Drift velocity is also related to the relaxation time (τ) by the equation:
vd∝τ
- As the temperature of the metal wire increases, the thermal agitation of the lattice ions increases, leading to more frequent collisions between electrons and lattice ions.
- This results in a decrease in the relaxation time (τ), which is the average time between collisions of the electrons. Therefore, we can conclude:
As temperature increases, τ decreases.
- Since drift velocity is directly proportional to relaxation time, if τ decreases, then:
vd decreases.
- The average thermal velocity (v_t) of electrons is related to their kinetic energy, which is influenced by temperature. As temperature increases, the kinetic energy of the electrons increases, leading to an increase in their average thermal velocity.
- Therefore, we can conclude:
As temperature increases, vt increases.
- As the temperature of the wire rises:
- The drift velocity vd decreases due to the decrease in relaxation time.
- The average thermal velocity vt increases due to increased kinetic energy.
- The correct answer is that as the temperature increases, the average thermal velocity vt increases while the drift velocity vd decreases.
Topper's Solved these Questions
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:LEVEL-1 DAILY TUTORIAL SHEET-2
Explore 15 Videos
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:LEVEL-1 DAILY TUTORIAL SHEET-3
Explore 15 Videos
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:LEVEL-0 LONG ANSWER TYPE
Explore 3 Videos
- CURRENT ELECTRICITYBook:VMC MODULES ENGLISHChapter:CURRENT ELECTRICITYExercise:IN-CHAPTER EXERCISE-F
Explore 10 Videos
- DYNAMICS OF A PARTICLEBook:VMC MODULES ENGLISHChapter:DYNAMICS OF A PARTICLEExercise:JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
Explore 31 Videos
Similar Questions
A constant voltage is applied across a wire of constant length then how drift velocity of electrons depends on area of cross-section of wire.
View SolutionConsider the following quantities: number density of free electrons, n, mean free time of electrons between collisions,t , drift velocity of electrons, vd , resistivity, p.
A constant potential difference is applied across a conductor. Assuming that the temperature of the conductor remains constant, which of these quantities is/are independent of the magnitude of the potential difference applied?
View SolutionA potential difference of 5 V is applied across a conductor of length 10 cm . If drift velcoity of electrons is 2.5×10−4m/s , then electron mobility will be
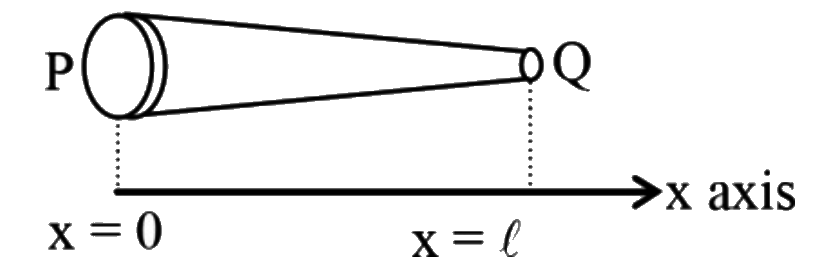
View SolutionA wire of length l tapers uniformly from end P to end Q with the diameter at P twice that at Q. A potential difference is applied across the ends of the wire. Which graph represents the variation of the drift velocity V of the conduction electrons with distance x?
View SolutionTwo different wires X and Y of same diameter but different materials are joined in series across a battery. If the number density of electrons in X is twice that in Y, find the ratio of drift velocity of electrons in the two wires .
View SolutionShows an irregular shaped wire AB moving with velocity v. Find the emf induced in the wire.

View SolutionShows an irregular shaped wire AB moving with velocity v. Find the emf induced in the wire.

View SolutionWhen a potential difference of 2 volt is applied across the ends of a wire of 5 m length, a current of 1 A flows through it. Calculate :
the resistance across the ends of the wire if it is doubled on itself.
View SolutionA constant voltage is applied between the two ends of a metallic wire . If both the length and the radius of the wire are doubled , the rate of heat developed in the wire will
View SolutionWhen a potential difference of 2 volt is applied across the ends of a wire of 5 m length, a current of 1 A flows through it. Calculate :
the resistance of 2 m length of the wire,
View Solution

