Question

In order to increase the resistance of a given wire of uniform cross section to four times its value, a fraction of its length is stretched uniformly till the full length of the wire becoes $\frac{3}{2}$ times the original length. What is the value of this fraction?

Explanation

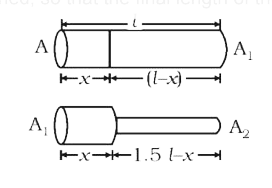
Let l be the original length of the wire. Suppose a portion of the wire is stretched, so that the final length of the whole wire becomes 1.5 l.
Let `R_1,R_2` be the resistance of the wire, before and after stretching. `A_1,A_2` be the area of cross-section of wire of portion of length x and (1.5 l – x) after stretching.
p is the resistivity of the material of wire.
As per Quesiton .`R_2=4R_1=(4pl)/A_1` (i) But `R_2=(p(1.51-x))/A_2+(px)/A_1=(4pl)/A_1`……(ii)
On stretching the wire, the total volume of the wire remains constants.
`therefore A_1l=A_2(1.51-x)+A_1x`………..(iii)
Solving Eqs. (ii) and (iii), we get `x/l=7/8`, Fraction of length of wire elongated )`=(1-x)/1=(8-7)/8=1/8`