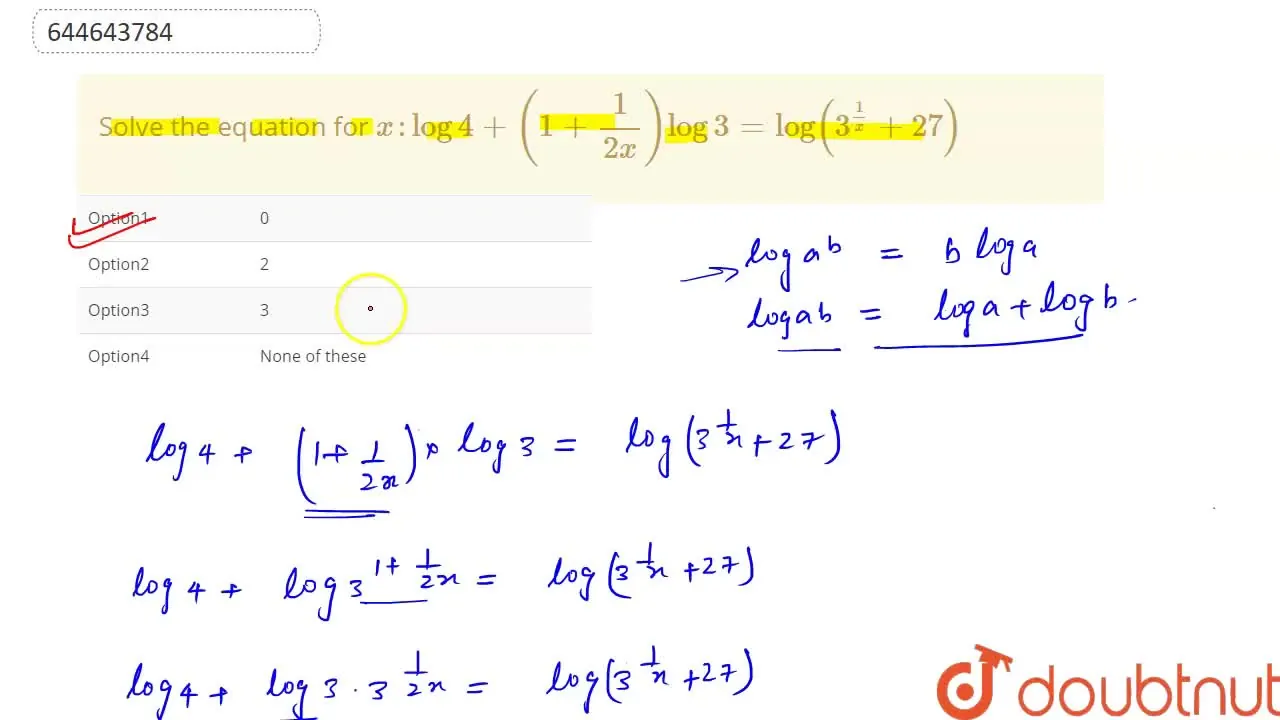
Solve the equation for x:log4+(1+12x)log3=log(31x+27)
0
2
3
None of these
The correct Answer is:A
Step by step video & image solution for Solve the equation for x : log4+(1+1/(2x))log3=log(3^(1/x)+27) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - VMC MODULES ENGLISHCHAPTER - FUNCTIONSEXERCISE - Level -247videos
FUNCTIONS
- BOOK - VMC MODULES ENGLISHCHAPTER - FUNCTIONSEXERCISE - Level -2 (Numerical Value Type for JEE Main)14videos
FUNCTIONS
- BOOK - VMC MODULES ENGLISHCHAPTER - FUNCTIONSEXERCISE - JEE Main & Advanced8videos
FUNCTIONS
- BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - JEE ADVANCE (ARCHIVE )32videos
DIFFERENTIAL EQUATIONS
- BOOK - VMC MODULES ENGLISHCHAPTER - INTEGRAL CALCULUS - 2 EXERCISE - JEE Advanced (Archive)103videos
INTEGRAL CALCULUS - 2
Similar Questions
Solve the equation: log(x+1)logx=2
View SolutionSolve the equation: log2x+log4(x+2)=2
View SolutionSolve the equation log(3x2+x−2)=3log(3x−2).
View SolutionSolve the equation: log2x+3x2<log2x(2x+3)
View SolutionSolve the equation log1/3[2(12)x−1]=log1/3[(14)x−4]
View SolutionSolve the following equation for x: 9log3(log2x)=log2x−(log2x)2+1
View SolutionSolve the equation log3(5+4log3(x−1))=2
View SolutionSolve the following equations for x and y: log10x+log10(x)12+log10(x)14+….=y 1+3+5+…+(2y−1)4+7+10+..+(3y+1)=207log10x
View SolutionSolve the equation 2xlog34+3logx4=27
View SolutionSolve the equations for xandy:(3x)log3=(4y)log4,4logx=3logy.
View Solution