Solve the equation: log2x+3x2<log2x(2x+3)
Video Solution
Text Solution
This inequation is equivalent to the collection of the systems
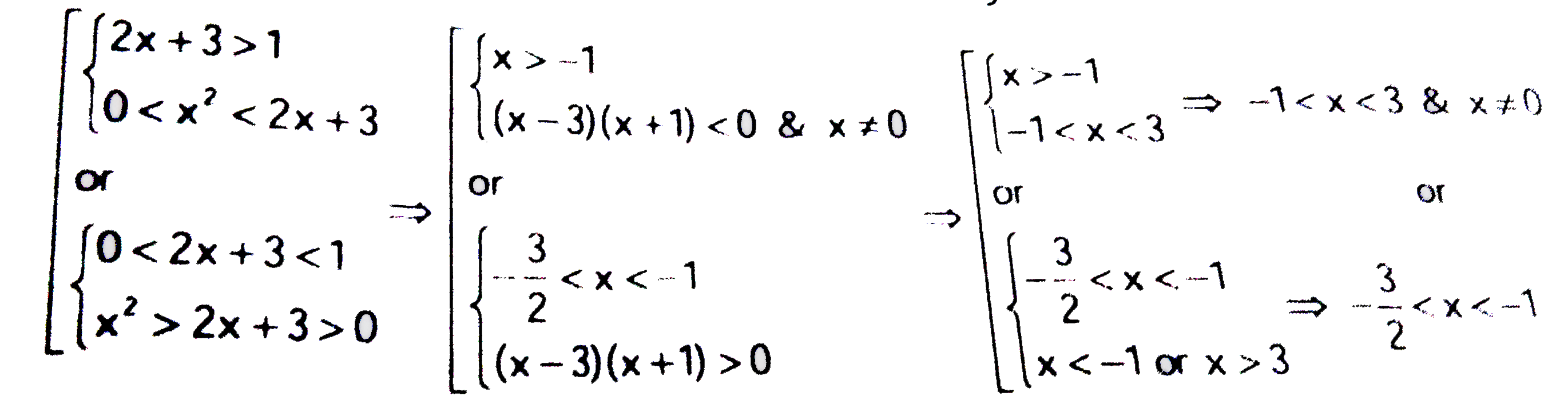
Hence, solution of the original inequation is x∈(−32,−1)∪(−1,0)∪(0,3)
|
Topper's Solved these Questions
Similar Questions
Solve the inequation log2x+3x2<log2x+3(2x+3)
View SolutionSolve the equation log(x3+6)(x2−1)=log(2x2+5x)(x2−1)
View SolutionSolve the equation: log2x+log4(x+2)=2
View SolutionSolve the equation xlogx(x+3)2=16.
View SolutionSolve the equation: 2log3x+log3(x2−3)=log30.5+5log5(log38)
View SolutionSolve the equation log4(2x2+x+1)−log2(2x−1)=1.
View SolutionSolve the equation:
log3x10−6log2x10+11logx10−6=0
View SolutionSolve the equation log(3x2+x−2)=3log(3x−2).
View SolutionSolve the equation log2(3−x)−log2⎛⎝sin3π45−x⎞⎠=12+log2(x+7)
View SolutionSolve the equation 2xlog34+3logx4=27
View Solution
