Consider a two particle system with the particles having masses m1andm2. If the first particles pushed towards the centre of mass through a distance d, by what distance should the second particle be moved so as the keep the centre of mass at the same position?
m2m1d
m1m1+m2d
m1m1d
d
The correct Answer is:C
To keep the centre of mass at the same position, velocity of centre of mass is zero, so
m1v1+m2v2m1+m2=0
Where, v1andv2 are the velocities of particles 1 and 2, respectively.
⇒m1dr1dt+m2dr2dt=0 [∵v1=dr1dtandv2=dr2dt]
⇒m1dr1+m1dr2=0
dr1anddr2 represent the change in displacement of particles.
Let 2ndpartic≤hasbeendisplacedbydistancex.impliesm1(d)+m2(x)=0 or x=−m1dm2 .
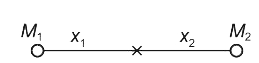
XCM=m1x1+m2x2m1+m2 .....(i)
After moving m1 through a distance towards CM and to keep the position of CM unchanged, let be the shift of m2.
XCM=m1(x1−d)+m2(x2+d')m1+m2 .....(iii)
From Eqs. (i) and (ii), we get
m1x1+m2x2m1+m2=m1(x1−d)+m2(x2+d)m1+m2⇒−m1d+m2d'=0 ∴ d'=m1m2d .
Topper's Solved these Questions
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE)
80 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - PARAGRAPH QUESTIONS
5 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - LEVEL - 2 PARAGRAPH QUESTIONS
2 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)
89 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )
111 Videos
Similar Questions
Consider a system of two particles having masses m1 and m2. If the particle of mass m1 is pushed towards the centre of mass of particles through a distance d, by what distance would the particle of mass m2 move so as to keep the mass centre of particles at the original position?
View SolutionConsider a sytem of two particles having masses m1 and m2. If the particle of mass m1 is pushed towards the centre of mass of particles through a distance d, by what distance would the particle of mass m2 move so as to keep the mass centre of particles at the original position?
View Solution
Knowledge Check
The reduce mass of two particles having masses m and 2 m is
A2 mB3 mC2 m/3Dm/2The centre of mass of a system of two particle of masses m1andm2 is at a distance d1 from mass m1 and at a distance d2 from mass m2 such that.
Ad1d2=m2m1Bd1d2=m1m2Cd1d2=m1m1+m2Dd1d2=m2m1+m2
Consider a system of two particles having masses 2kg and 5 kg the particle of mass 2 kg is pushed towards the centre of mass of particles through a distance 5 m,by what distance would particle of mass 5kg move so as to keep the centre of mass of particles at the original position?
View SolutionConsidering a system having two masses m1 and m2 in which first mass is pushed towards centre of mass by a distance a, the distance required to be moved for second mass to keep centre of mass at same position is :-

View SolutionTwo bocks of masses 10 g and 20 kg are plced on the X-axis. The first mass is moved on the axis by a distance of 2 cm. By what distance should the second mass be moved to keep the position of the centre of mass unchanged?
View SolutionConsider a system of two identical particles. One of the particles is at rest and the other has an acceleration. The centre of mass has an acceleration.
View SolutionThe coordinates of the centre of mass of a system of three particles of masses 1 mg , 2 mg and 3mg are (2 ,2 ,2) . The coordinates of the fourth particle of mass 4 mg to be positioned so that the center of mass of the four particles system is at the origin of the three – dimensional rectangular coordinate system are
View SolutionFour identical particles each of mass m are arranged at the corners of a square of sie a. If mass of one of th particle is doubled, the shift in the centre of mass of the system is
View Solution
