A block of mass 2 kg is hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force F = 40 N. The kinetic energy of the particle increases 40 J in a given interval of time. Then, (g=10m/s2)
Tension in the string is 40 N
Displacement of the block in the given interval of time is 2m
Workdone by gravity is –20 J
Workdone by tension is 80 J
The correct Answer is:A, B, D
To solve the problem step by step, we will analyze the forces acting on the block and apply the work-energy principle.
Step 1: Identify the forces acting on the block
The forces acting on the block of mass m=2kg are:
1. The weight of the block acting downwards:
W=m⋅g=2kg⋅10m/s2=20N
2. The tension T in the string acting upwards.
The problem states that a constant force F=40N is pulling the other end of the string.
Step 2: Apply the Work-Energy Principle
According to the work-energy principle, the net work done on the block is equal to the change in kinetic energy. We know that the kinetic energy increases by 40J.
The net work done Wnet can be expressed as:
Wnet=Wtension+Wgravity
Where:
- Wtension is the work done by the tension.
- Wgravity is the work done by gravity.
Step 3: Calculate the work done by gravity
The work done by gravity when the block moves a distance s downwards is given by:
Wgravity=−W⋅s=−20N⋅s
Since we need to find the displacement s, we will calculate it later.
Step 4: Calculate the work done by tension
The work done by tension when the block moves a distance s upwards is given by:
Wtension=T⋅s=T⋅s
Where T is the tension in the string.
Step 5: Set up the equation
From the work-energy principle:
Wnet=Wtension+Wgravity=40J
Substituting the expressions for work:
T⋅s−20⋅s=40
This simplifies to:
(T−20)⋅s=40
Step 6: Determine the tension in the string
Since the force F=40N is pulling the string, and the system is in equilibrium, the tension T in the string must also be equal to 40N.
Step 7: Substitute the tension value
Substituting T=40N into the equation:
(40−20)⋅s=40
This simplifies to:
20⋅s=40
Thus,
s=4020=2m
Step 8: Calculate work done by tension
Now, we can calculate the work done by tension:
Wtension=T⋅s=40N⋅2m=80J
Final Results
1. The displacement of the block s=2m.
2. The work done by tension Wtension=80J.
3. The work done by gravity Wgravity=−20⋅2=−40J.
Summary
- Tension in the string: 40N
- Displacement of the block: 2m
- Work done by gravity: −40J
- Work done by tension: 80J
The forces acting on the block of mass m=2kg are:
1. The weight of the block acting downwards:
W=m⋅g=2kg⋅10m/s2=20N
2. The tension T in the string acting upwards.
According to the work-energy principle, the net work done on the block is equal to the change in kinetic energy. We know that the kinetic energy increases by 40J.
Wnet=Wtension+Wgravity
Where:
- Wtension is the work done by the tension.
- Wgravity is the work done by gravity.
The work done by gravity when the block moves a distance s downwards is given by:
Wgravity=−W⋅s=−20N⋅s
Since we need to find the displacement s, we will calculate it later.
The work done by tension when the block moves a distance s upwards is given by:
Wtension=T⋅s=T⋅s
Where T is the tension in the string.
From the work-energy principle:
Wnet=Wtension+Wgravity=40J
Substituting the expressions for work:
T⋅s−20⋅s=40
This simplifies to:
(T−20)⋅s=40
Since the force F=40N is pulling the string, and the system is in equilibrium, the tension T in the string must also be equal to 40N.
Substituting T=40N into the equation:
(40−20)⋅s=40
This simplifies to:
20⋅s=40
Thus,
s=4020=2m
Now, we can calculate the work done by tension:
Wtension=T⋅s=40N⋅2m=80J
1. The displacement of the block s=2m.
2. The work done by tension Wtension=80J.
3. The work done by gravity Wgravity=−20⋅2=−40J.
- Tension in the string: 40N
- Displacement of the block: 2m
- Work done by gravity: −40J
- Work done by tension: 80J
Topper's Solved these Questions
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - LEVEL - 2 PARAGRAPH QUESTIONS
2 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE MAIN (ARCHIVE)
53 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - Level - 1 PARAGRAPH QUESTIONS
3 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)
89 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )
111 Videos
Similar Questions
A block of mass M is hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force F. The kinetic energy of the block increases by 20J in 1s.
View SolutionA block of mass 10 kg is hanging over a smooth and light pulley through a light string and the other end of the string is pulled down by a constant force F. The kinetic energy of the block increases by 20 J in 1 s
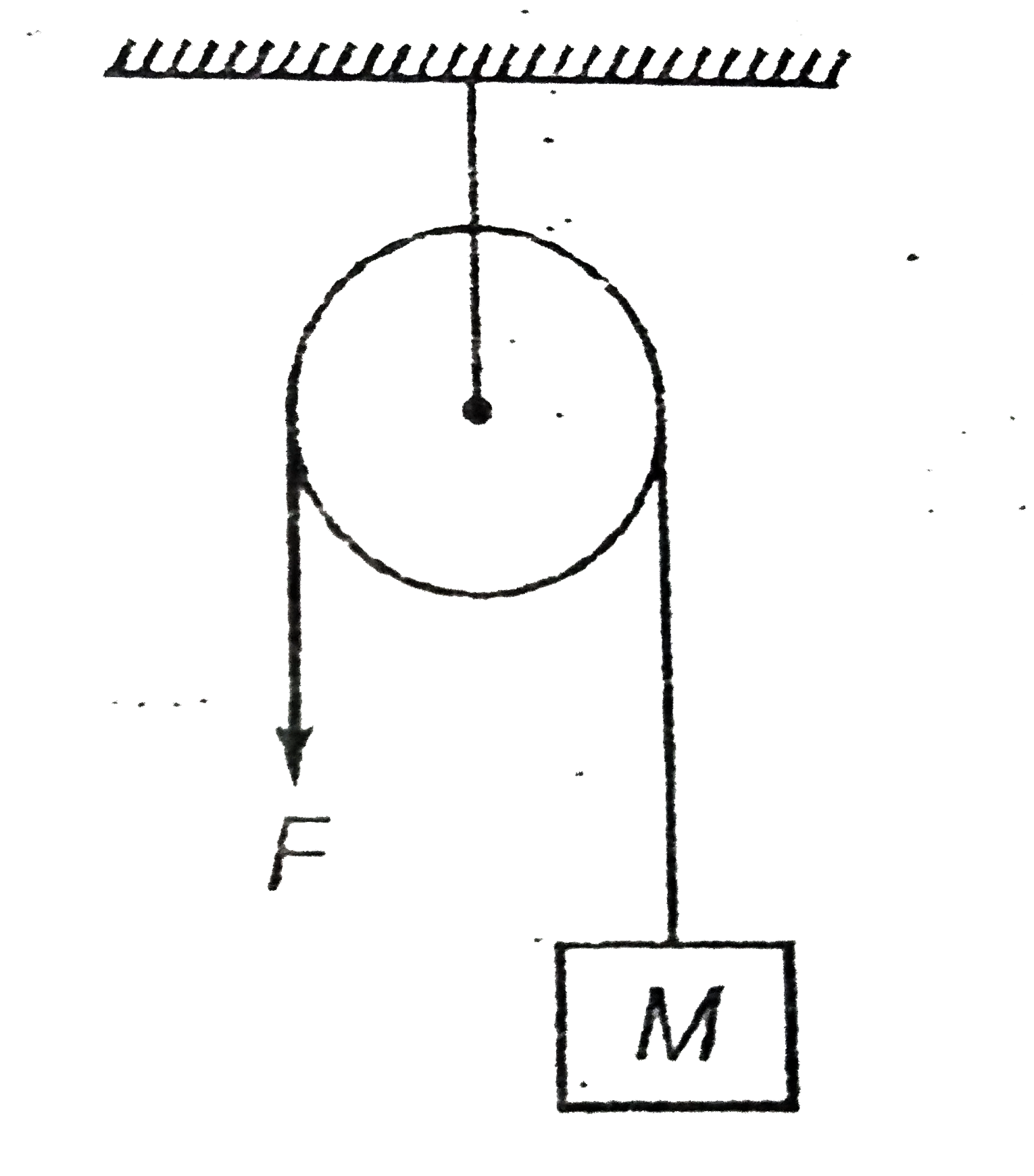
View SolutionA block of mass M hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force F. The kinetic of the block increases by 40J in 1s. State whether the following statements are true or false.
(a) The tension in the string is Mg .
(b) The work done the tension on the block is 40J.
(c) the tension in the string is F.
(d) The work done by the force of gravity is 40J in the above 1s .
View SolutionA block of mass 2kg is hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force F=40N . At t=0 the system is at rest as shown. Then in the time interval from t=0 to t=2√10 seconds, pick up the correct statement (s):(g=10m/s2)
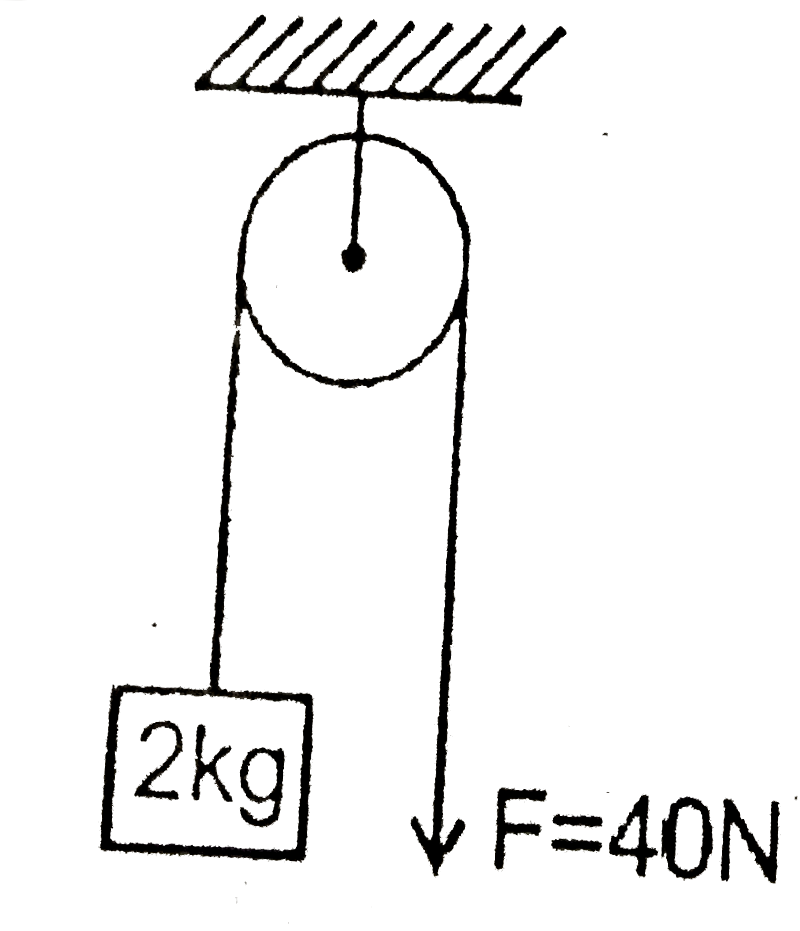
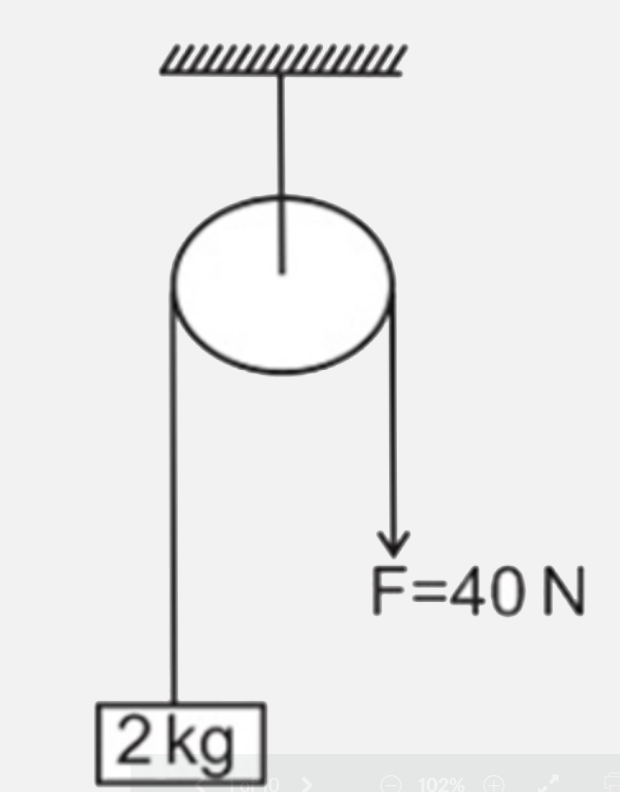
View SolutionIn the system shown in the figure, the block is pulled by applying a force of 40 N on the other end of the string. If the kinetic energy of the block increases by 40 J in a given interval of time then work done by tension on the block is (g=10ms−2)
View Solution
In the shown mass pulley system, pulleys and string are massless. The one end of the string is pulleed by the force F=2mg. The acceleration of the block will be
View Solution
In the shown mass pulley system, pulleys and string are massless. The one end of the string is pulleed by the force F=2mg. The acceleration of the block will be
View SolutionTwo blocks of equal mass m are tied to each other through light string. One of the blocks is pulled along the line joining them with a constant force F. Find the tension in the string joining the blocks.
View SolutionA 1m long rope, having a mass of 40g, is fixed at one end and is tied to a light string at the other end. The tension in the string in 400N. Find the wavelength in second overtone (in cm).
View SolutionA bob is hanging over a pulley inside a car through a string. The second end of the string is in the hands of a person standing in the car. The car is moving with constant acceleration a directed horizontally as shown in fig. The other end of the string is pulled with constant acceleration a vertically. The tension in the string is equal to

View Solution
