Question

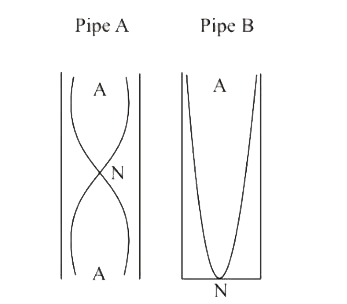
Two narrow cylindrical pipes $A$ and $B$ have the same length. Pipe $A$ is open at both ends and is filled with a monoatomic gas of molar mass $M_A$. Pipe $B$ is open at one end and closed at the other end and is filled with a diatomic gas of molar mass $M_B$. Both gases are at the same temperature.
(a) If the frequency of the second harmonic of the fundamental mode in pipe $A$ is equal to the frequency of the third harmonic of the fundamental mode in pipe $B$, determine the value of $\frac{m_A}{M_B}$.
(b) Now, the open end of pipe $B$ is also closed (so that the pipe is closed at both ends.) Find the ratio of the fundamental frequency in pipe $A$ to that in pipe $B$.

Answer

(i) `(400)/(189),(ii)(3)/4`

Explanation

(i)If L is the length of each pipe A and B,the fundamental frequency of pipe A (pen both ends)
`n_A=(V_A)/(2L)`…..(i)
Fundamental frequency of B(closed at one end )
`n_B=(V_B)/(4L)`…(ii)
Given `2n_a=3 n_B`
`2((V_A)/(2L))=3((V_s)/(4L))`
`implies (V_A)/(V_B)=3/4`.....(iii)
But `V_A=sqrt((gamma_ART_A)/(M_A)),V_B=sqrt((gammaRT_B)/(M_B)))`
Given `T_A=T_B`
For monoatomic get `gamma_A=5/3`
For diatomic `gamma_B=7/5therefore V_A/(V_B)=sqrt((gamma_AM_B)/(gamma_(B)M_B))=sqrt((5//3M_B)/((7//5)M_A))`,br> `sqrt(25/21(M_B)/(M_A))`....(iv)
From Eqs (iii) and (Iv)
`sqrt(25/21(M_B)/(M_A))=3/4, (M_A)/(M_B)=((4)/(3))^(2)xx25/11=400/189`
When pipe B is closed at both ends,fundamental frequency of pipeB becomes
`n_B=(V_B)/(2L)`..(iv)
Using Eqs (i),(iii) and (v) we get
`n_A/(n_B)=V_A/(V_B)=3/4`