Question

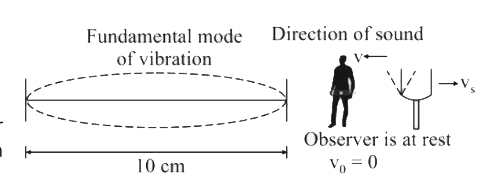
A sonometer wire under tension of 64 N vibrating in its fundamental mode is in resonance with a vibrating tuning fork. The vibrating portion of the sonometer wire has a length of 10 cm and mass of 1 g. The vibrating tuning fork is now moved away from the vibrating wire with a constant speed and an observer standing near the sonometer hears one beat per second. Calculate the speed with which the tuning fork is moved, if the speed of sound in air is 300 m/s.

Answer

0.752

Explanation

Linear mass density of sonometer wire `mu=m/1=0.001/0.1=0.01 kh//m`
Velocity wave `v=sqrt((T)/(mu))=sqrt((64)/(0.01))=80 m//s`
For fundamental frequency
Also, `(lambda)/2=0.1implies =0.2 therefore f=v/(lambda)=80/0.2=400 Hz` since tuning forks is in resonance ,therefore frequency of tuning fork is 400 Hz.The observer is hearing one beat per second when the tuning fork is moved away with constant speed v.
, The frequency of tuning fork as heard by the observer standing staionary near sonometer wire can be found with the help of doppler effect.
Using `f'=f_0[(v-v_0)/(v-(-v_s))]=(vf_0)/(v+v_s) therefore f'(400xx300)/(300+v_s)`
Since the beat frequency is 1 and as the tuning fork is going away from the observer,its apparent frequency should be 399 Hz.
`therefore 399=(400xx300)/(300+v_s)implies v_s=300/399=0.752 m//s`