What is the phase relationship between diplacement, velocity and acceleration in SHM?
To determine the phase relationship between displacement, velocity, and acceleration in Simple Harmonic Motion (SHM), we can follow these steps:
1. Define Displacement in SHM:
The displacement x in SHM can be expressed as:
x(t)=asin(ωt)
where a is the amplitude and ω is the angular frequency.
2. Calculate Velocity:
The velocity v is the time derivative of displacement:
v(t)=dxdt=ddt(asin(ωt))=aωcos(ωt)
3. Calculate Acceleration:
The acceleration a is the time derivative of velocity:
a(t)=dvdt=ddt(aωcos(ωt))=−aω2sin(ωt)
4. Identify Phase Relationships:
- The displacement x(t)=asin(ωt) is at its maximum when sin(ωt)=1.
- The velocity v(t)=aωcos(ωt) reaches its maximum when cos(ωt)=1, which occurs π2 radians (or 90∘) after the maximum displacement.
- The acceleration a(t)=−aω2sin(ωt) is opposite in direction to displacement and reaches its maximum when displacement is at its maximum.
5. Summarize Phase Differences:
- The phase difference between displacement x and velocity v is:
Phase difference=π2 radians (or 90∘)
- The phase difference between velocity v and acceleration a is also:
Phase difference=π2 radians (or 90∘)
- The phase difference between displacement x and acceleration a is:
Phase difference=π radians (or 180∘)
Final Result:
- Displacement and velocity have a phase difference of π2 radians.
- Velocity and acceleration have a phase difference of π2 radians.
- Displacement and acceleration have a phase difference of π radians.
The displacement x in SHM can be expressed as:
x(t)=asin(ωt)
where a is the amplitude and ω is the angular frequency.
The velocity v is the time derivative of displacement:
v(t)=dxdt=ddt(asin(ωt))=aωcos(ωt)
The acceleration a is the time derivative of velocity:
a(t)=dvdt=ddt(aωcos(ωt))=−aω2sin(ωt)
- The displacement x(t)=asin(ωt) is at its maximum when sin(ωt)=1.
- The velocity v(t)=aωcos(ωt) reaches its maximum when cos(ωt)=1, which occurs π2 radians (or 90∘) after the maximum displacement.
- The acceleration a(t)=−aω2sin(ωt) is opposite in direction to displacement and reaches its maximum when displacement is at its maximum.
- The phase difference between displacement x and velocity v is:
Phase difference=π2 radians (or 90∘)
- The phase difference between velocity v and acceleration a is also:
Phase difference=π2 radians (or 90∘)
- The phase difference between displacement x and acceleration a is:
Phase difference=π radians (or 180∘)
- Displacement and velocity have a phase difference of π2 radians.
- Velocity and acceleration have a phase difference of π2 radians.
- Displacement and acceleration have a phase difference of π radians.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:LEVEL 0 SHORT ANSWER TYPE - I
Explore 8 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:LEVEL 0 SHORT ANSWER TYPE - II
Explore 12 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (True/False Type)
Explore 3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF A PARTICLES & ROTATIONAL MOTIONExercise:IN-CHAPTER EXERCISE F
Explore 10 Videos
Similar Questions
What is the relationship between KpandKc ?
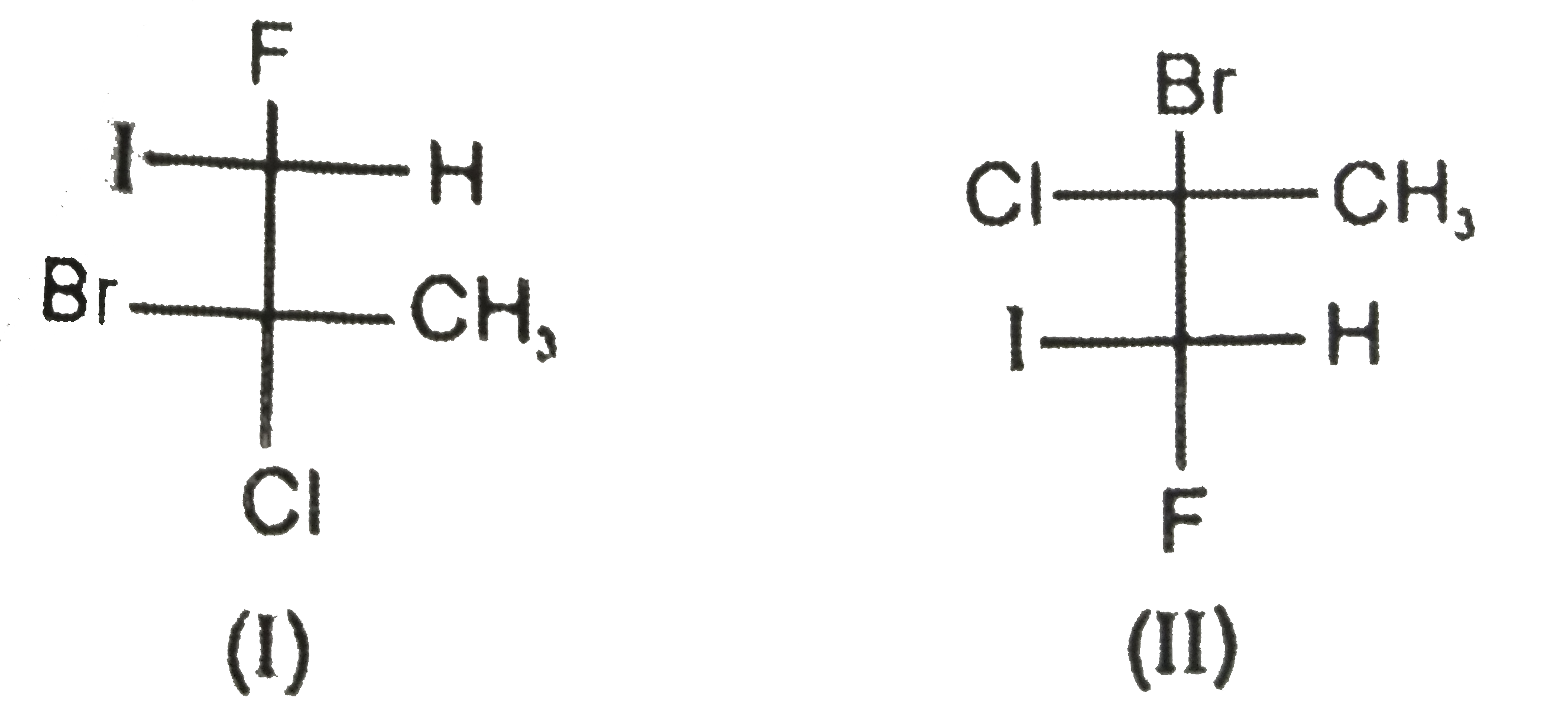
View SolutionWhat is the relationship between (I) & (II)
View SolutionWhat is the direction of velocity and acceleration in shm ?
View SolutionWhat is the relationship between ∠AON and ∠NOB?
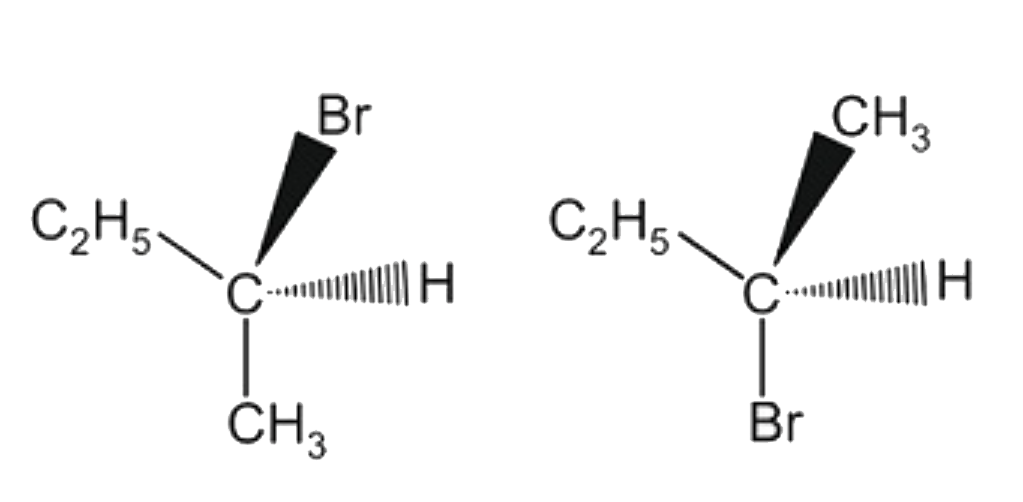
View SolutionWhat is the relationship between the structure below?
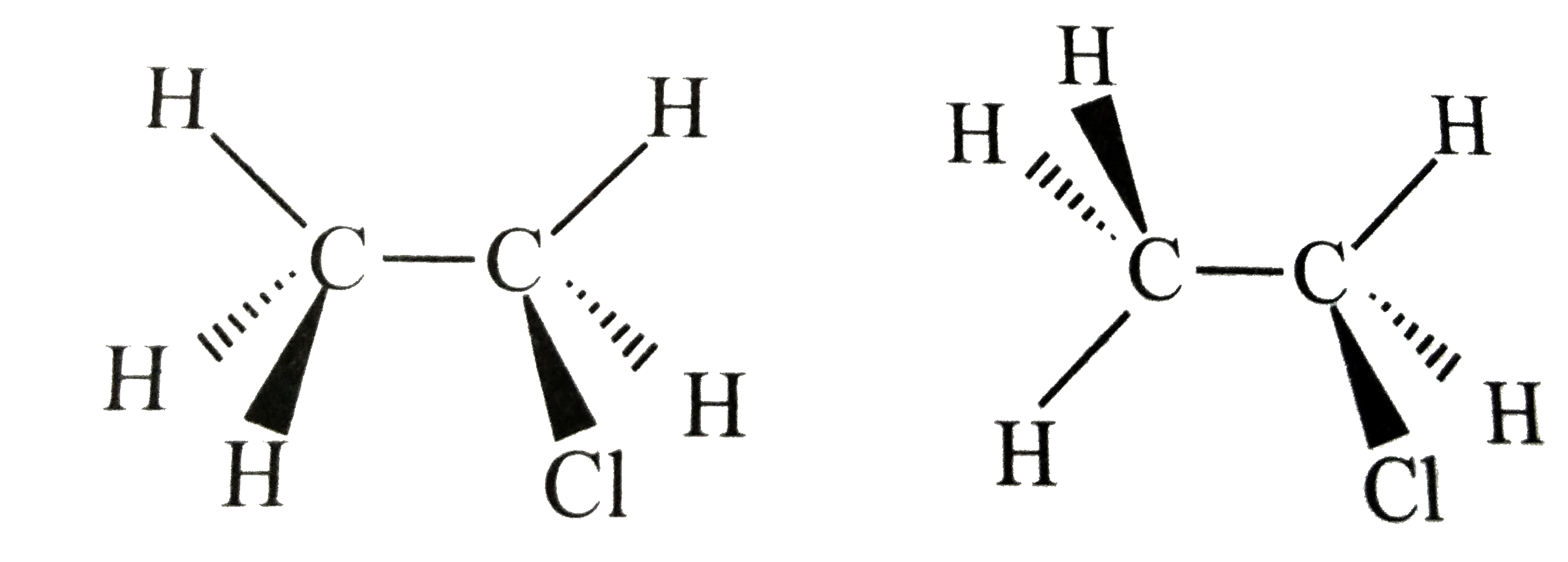
View SolutionWhat is the relationship between the structures shown ?
View SolutionWhat is the direction of displacement and acceleration in shm?
View SolutionWhat is the relationship between pKa and Ka of an acid ?
View SolutionWhat is the relationship between pKa and Ka of an acid ?
View SolutionWhat is the relationship between pKa and Ka of an acid ?
View Solution
