A glass container encloses gas at a pressure 4×105 Pa and 300 K temperature. The container walls can bear a maximum pressure of 8×105 Pa. If the temperature of container is gradually increased find temperature at which container will break.
600K
150K
1200K
375K
The correct Answer is:A
To solve the problem, we will use Gay-Lussac's Law, which states that the pressure of a gas is directly proportional to its absolute temperature when the volume is constant. The relationship can be expressed as:
P1P2=T1T2
Where:
- P1 = initial pressure of the gas
- P2 = maximum pressure the container can withstand
- T1 = initial temperature of the gas
- T2 = temperature at which the container will break
1. Identify the Given Values:
- Initial pressure, P1=4×105 Pa
- Maximum pressure, P2=8×105 Pa
- Initial temperature, T1=300 K
2. Set Up the Equation Using Gay-Lussac's Law:
P1P2=T1T2
3. Substitute the Known Values into the Equation:
4×1058×105=300T2
4. Simplify the Left Side:
48=12
So the equation becomes:
12=300T2
5. Cross-Multiply to Solve for T2:
1⋅T2=2⋅300
T2=600 K
6. Conclusion:
The temperature at which the container will break is T2=600 K.
Final Answer:
The temperature at which the container will break is 600 K.
- P1 = initial pressure of the gas
- P2 = maximum pressure the container can withstand
- T1 = initial temperature of the gas
- T2 = temperature at which the container will break
- Initial pressure, P1=4×105 Pa
- Maximum pressure, P2=8×105 Pa
- Initial temperature, T1=300 K
P1P2=T1T2
4×1058×105=300T2
48=12
So the equation becomes:
12=300T2
1⋅T2=2⋅300
T2=600 K
The temperature at which the container will break is T2=600 K.
The temperature at which the container will break is 600 K.
Topper's Solved these Questions
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:Level - 2
Explore 40 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE MAIN (ARCHIVE )
Explore 81 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:level-0 Short Answer Type – II
Explore 24 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
Explore 1 Video
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive) TRUE/FALSE
Explore 1 Video
Similar Questions
A glass container encloses a gas a pressure of 8×105 pa and 300 K temperature. The container walls can bear a maximum pressure of 106 Pa. If the temperature of container is gradually increased, find the temperature at which the container will break.
View SolutionIncrease in temperature of a gas filled in a container would lead to :
View Solution
Knowledge Check
A cylinder contained 10kgof gas at pressure 107Nm2. The quantity of gas taken out of cylinder if final pressure is 2.5×106N/m2 is (Assume temperature of gas is constant)
A9.5 kgB7.5 kgC14.2 kgDzero
An iron cylinder contains helium at a pressure of 250 k Pa at 300 K. The cylinder can withstand a pressure of 1×106 Pa. The room in which cylinder is placed catches fire. Predict the temperature (in K) at which the cylinder will blow up before it melts or not (m.p.t. of the cylinder =1800K)..
View SolutionA closed box contains an ideal gas if temperature of gas increased which
View SolutionA 0.50 L container is ocupied by nitrogen at a pressure of 800 torr and a temperature of 0∘C. The container can only withstand a pressure of 3.0 atm. What is the highest temperature (∘C) to which the container may be heated?
View SolutionThe temperature of a gas contained in a closed vessel increases by 1∘C when pressure of the gas is increased by 1%. The initial temperature of the gas is
View SolutionContainer A holds an ideal gas at a pressure 1×105 Pa and at 300 K. Container B whose volume is 4 times the volume of A has the same ideal gas at 400 K and at a pressure of 5×105
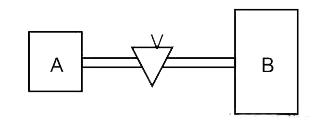
The valve V is adjusted to allow the pressure to equalize, but the temperature of each container is kept constant at the initial value, then the pressure in the two containers is :
View SolutionA cylinder contains 12kg of gas at pressure of 107 N/m2. The quantity of gas taken out of the cylinder, if final pressure is 3×106N/m2 , will be (temperature of gas is constant)
View SolutionA gas cylinder has walls that can bear a maximum pressure of 1.0×106Pa. It contains a gas at 8.0×105Pa and 300K. The cylinder is steadily heated. Neglecting any change in the volume calculate the temperature at which the cylinder will break.
View Solution
