For a p-V plot, the slope of an adiabatic curve = x × slope of isothermal at the same point. Here x is :
(a)Rλ−1
(b)1λ
(c)λ
(d)1λ−1
The correct Answer is:C
To solve the problem, we need to determine the relationship between the slopes of the adiabatic and isothermal curves on a p-V plot.
1. Understand the Isothermal Process:
- For an isothermal process, the temperature (T) remains constant. The equation for an isothermal process is given by:
PV=nRT
- Taking the differential of this equation gives us:
d(PV)=0⟹PdV+VdP=0
- Rearranging this, we find:
dPdV=−PV
- This indicates that the slope of the isothermal curve at any point is:
slopeisothermal=−PV
2. Understand the Adiabatic Process:
- For an adiabatic process, there is no heat exchange (Q = 0). The relationship for an adiabatic process is given by:
PVγ=constant
- Here, γ (gamma) is the adiabatic index, which is the ratio of specific heats (Cp/Cv).
- Taking the differential of this equation gives us:
d(PVγ)=0⟹Pd(Vγ)+VγdP=0
- Using the product rule, we can express d(Vγ) as:
γPVγ−1dV+VγdP=0
- Rearranging gives:
dP=−γPVdV
- Thus, the slope of the adiabatic curve at any point is:
slopeadiabatic=−γPV
3. Relate the Slopes:
- Now, we can relate the slopes of the adiabatic and isothermal curves:
slopeadiabatic=γ×slopeisothermal
- Therefore, we can express this as:
slopeadiabatic=γ(−PV)
4. Conclusion:
- From the relationship derived, we see that:
x=γ
- Hence, the value of x is equal to the adiabatic index γ.
Final Answer:
The value of x is γ.
- For an isothermal process, the temperature (T) remains constant. The equation for an isothermal process is given by:
PV=nRT
- Taking the differential of this equation gives us:
d(PV)=0⟹PdV+VdP=0
- Rearranging this, we find:
dPdV=−PV
- This indicates that the slope of the isothermal curve at any point is:
slopeisothermal=−PV
- For an adiabatic process, there is no heat exchange (Q = 0). The relationship for an adiabatic process is given by:
PVγ=constant
- Here, γ (gamma) is the adiabatic index, which is the ratio of specific heats (Cp/Cv).
- Taking the differential of this equation gives us:
d(PVγ)=0⟹Pd(Vγ)+VγdP=0
- Using the product rule, we can express d(Vγ) as:
γPVγ−1dV+VγdP=0
- Rearranging gives:
dP=−γPVdV
- Thus, the slope of the adiabatic curve at any point is:
slopeadiabatic=−γPV
- Now, we can relate the slopes of the adiabatic and isothermal curves:
slopeadiabatic=γ×slopeisothermal
- Therefore, we can express this as:
slopeadiabatic=γ(−PV)
- From the relationship derived, we see that:
x=γ
- Hence, the value of x is equal to the adiabatic index γ.
The value of x is γ.
Topper's Solved these Questions
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - Level - 2
40 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE MAIN (ARCHIVE )
81 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - level-0 Short Answer Type – II
24 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Video
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) TRUE/FALSE
1 Video
Similar Questions
Knowledge Check
The relation between the slope of isothemal curve and slope of adiabatic curve
Aa. slope of adiabatic curve =γ times slope of isotharmal curveBb.slope of isothermal curve =γ times slope of adiabatic curveCc.slope of adiabatic curve =γ2 times slope of isothermal curveDd. slope of isothermal curve =γ2 times slope of adiabatic curve
What is the slope for an isothermal process ?
View SolutionAssertion: Isothermal and adiabatic, two processes are shown on p-V diagram. Process-1 is aidabatic and process-2 is isothermal.
Reason: At a given point, slope of adiabatic process =γ×slope of isothermal process.
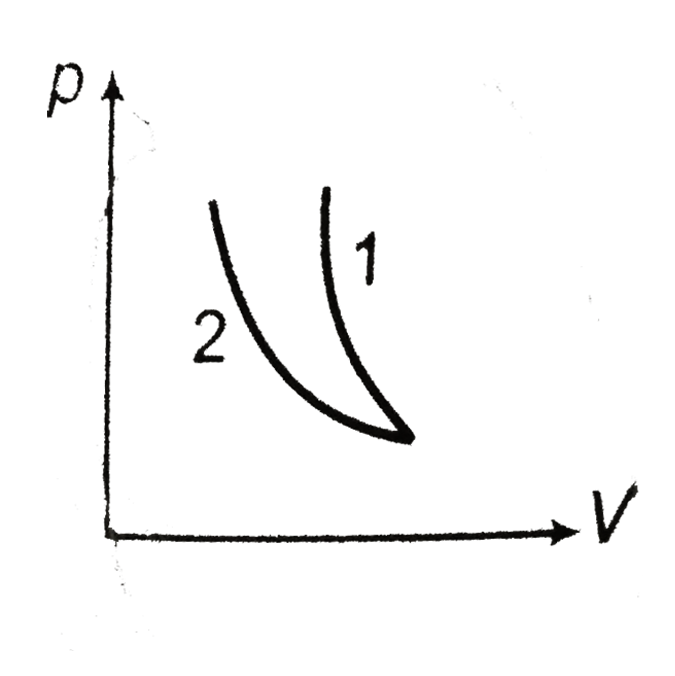
View SolutionShow that the adiabatic curve is steeper than the isothermal curve.
View SolutionStatement-1: Temperature of a system can be increased without supplying heat.
Statement-2: If the initial volume of system is equal to final volume in a process then work done is necessarily zero.
Statement-3: If an adiabatic curve for a gas intersect with an isothermal curve for the same gas then at the point of intersection, the ratio of slope of the adiabatic and the isothermal curve is γ.
View SolutionIf the slope for isotherm is X and the slope for adiabat is Y then
View SolutionA curve in the first quadrant is such that the slope of OP is twice the slope of the tangent drawn at P to the curve, where O is the origin and P is any general point on the curve. If the curve passes through (4, 2), then its equation is
View SolutionThe slope of the tangent of the curve y=∫x0dx1+x3 at the point where x=1 is
View Solution
