A spherical body of radius R consists of a fluid of constant density and is in equilibrium under its own gravity. If P(r) is the pressure at r (r < R), then the correct option(s) is (are)
P(r=0)=0
P(r=3R/4)P(r=2R/3)=6380
P(r=3R/5)P(r=2R/5)=1621
P(r=R/2)P(r=R/3)=2027
The correct Answer is:B, C
To solve the problem, we need to find the pressure P(r) at a distance r from the center of a spherical body of radius R that consists of a fluid of constant density and is in equilibrium under its own gravity.
1. Understanding the Problem:
- We have a spherical body of radius R filled with a fluid of constant density ρ.
- We need to find the pressure P(r) at a point inside the sphere at a distance r from the center, where r<R.
2. Consider a Shell:
- Consider a thin spherical shell of thickness dr at a distance r from the center. The inner pressure at this shell is P(r) and the outer pressure is P(r)+dP.
3. Hydrostatic Equilibrium:
- According to hydrostatic equilibrium, the change in pressure across the shell is given by:
P(r)−(P(r)+dP)=−ρgdr
- This simplifies to:
−dP=ρgdr
4. Expression for Acceleration due to Gravity g:
- The acceleration due to gravity g at a distance r from the center of the sphere is given by:
g=GM(r)r2
- Where M(r) is the mass enclosed within the radius r:
M(r)=ρ⋅Volume=ρ⋅43πr3
- Thus,
g=Gρ⋅43πr3r2=43πGρr
5. Substituting g into the Pressure Equation:
- Now substituting g back into the pressure equation:
−dP=ρ(43πGρr)dr
- This gives:
dP=−43πGρ2rdr
6. Integrating to Find Pressure:
- Integrate both sides from R to r:
∫P(r)P(R)dP=−43πGρ2∫rRrdr
- The left side becomes P(r)−P(R) and the right side becomes:
−43πGρ2(r22)rR=−43πGρ2(r22−R22)
- Therefore, we have:
P(r)−P(R)=−43πGρ2(r2−R22)
7. Finding P(R):
- At the surface r=R, the pressure P(R) is usually taken as zero (atmospheric pressure or reference pressure). Thus:
P(r)=43πGρ2(R2−r22)
8. Final Expression:
- The final expression for pressure at a distance r from the center is:
P(r)=23πGρ(R2−r2)
Conclusion:
The pressure P(r) at a distance r from the center of the sphere is proportional to the difference between the square of the radius of the sphere and the square of the distance r.
- We have a spherical body of radius R filled with a fluid of constant density ρ.
- We need to find the pressure P(r) at a point inside the sphere at a distance r from the center, where r<R.
- Consider a thin spherical shell of thickness dr at a distance r from the center. The inner pressure at this shell is P(r) and the outer pressure is P(r)+dP.
- According to hydrostatic equilibrium, the change in pressure across the shell is given by:
P(r)−(P(r)+dP)=−ρgdr
- This simplifies to:
−dP=ρgdr
- The acceleration due to gravity g at a distance r from the center of the sphere is given by:
g=GM(r)r2
- Where M(r) is the mass enclosed within the radius r:
M(r)=ρ⋅Volume=ρ⋅43πr3
- Thus,
g=Gρ⋅43πr3r2=43πGρr
- Now substituting g back into the pressure equation:
−dP=ρ(43πGρr)dr
- This gives:
dP=−43πGρ2rdr
- Integrate both sides from R to r:
∫P(r)P(R)dP=−43πGρ2∫rRrdr
- The left side becomes P(r)−P(R) and the right side becomes:
−43πGρ2(r22)rR=−43πGρ2(r22−R22)
- Therefore, we have:
P(r)−P(R)=−43πGρ2(r2−R22)
- At the surface r=R, the pressure P(R) is usually taken as zero (atmospheric pressure or reference pressure). Thus:
P(r)=43πGρ2(R2−r22)
- The final expression for pressure at a distance r from the center is:
P(r)=23πGρ(R2−r2)
The pressure P(r) at a distance r from the center of the sphere is proportional to the difference between the square of the radius of the sphere and the square of the distance r.
Topper's Solved these Questions
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive)ASSERTIOIN AND REASON
1 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive)MATCH MATRIX
1 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) SINGLE OPTION CORRECT
14 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )
111 Videos
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Advanced ( ARCHIVE LEVEL-2)
12 Videos
Similar Questions
Knowledge Check
Consider a thin spherical shell of radius R consisting of uniform surface charge density σ. The electric field at a point of distance x from its centre and outside the shell is
Ainversely proportional to σBdirectly proportional to x2Cdirectlr proportional to RDinversely proportional to x2Energy needed in breaking a drop of radius R into n drops of radius r, is where T is surface tension and P is atmospheric pressure.
A(4πr2n−4πR2)TB(4π3nr2−43πR2)TC(4πR2−4πr2)nTD(4πR2−n4πr2)P
Assuming the sun to be a spherical body (e = 1) of radius R at a temperature of T K, evaluate the total radiant power, incident on Earth having radius r0, at a distance r from the sun, where r0 is the radius of the earth and σ is Stefan's constant.
View SolutionA cylinder of radius R full of liquid of density p is rotated about its axis at w rad/s. The increase in pressure at the centre of the cylinder will be
View SolutionA solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View SolutionThe gravitational force between a hollow spherical shell (of radius R and uniform density) and a point mass is F. Show the nature of F versus r graph where r is the distance of the point from the centre of the hollow spherical shell of uniform density
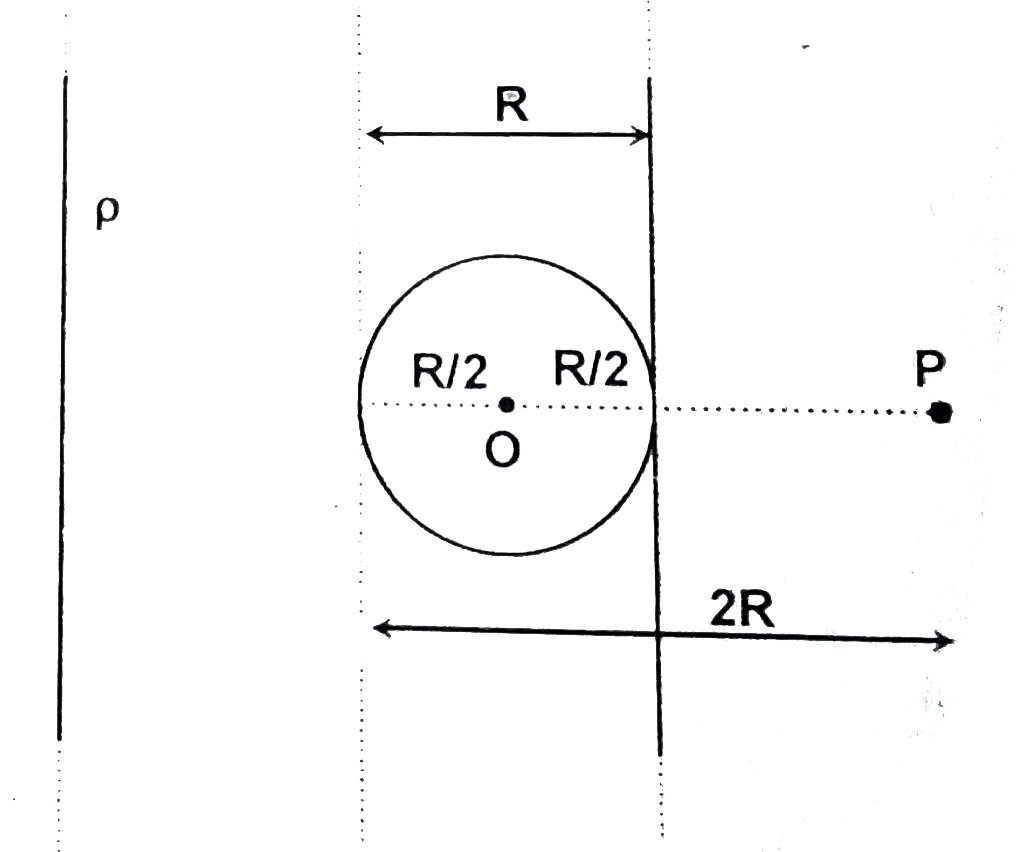
View SolutionInside a uniformly charged infinitely long cylinder of radius 'R' and volume charge density 'rho' there is a spherical cavity of radius 'R//2'. A point 'P' is located at a dsintance 2R from the axis of the cylinder as shown. Then the electric field strength at the point 'P' is
View SolutionA star can be considered as spherical ball of hot gas of radius R. Inside the star, the density of the gas is ρr at radius r and mass of the gas within this region is Mr.
The correct differential equation for variation of mass with respect to radius is (refer to the adjacent figure)
View Solution
