Two spherical planets P and Q have the same uniform density ρ, masses MP and MQ and surface areas A and 4A, respectively. A spherical planet R also has uniform density ρ and its mass is (MP+MQ). The escape velocities from the planets P,Q and R, are VP,VQ and VR, respectively.
VQ>VR>VP
VR>VQ>VP
VR/VP=3
VP/VQ=1/2
The correct Answer is:B, D
Ves=√2GMR=√2Gr.43pR3R=√8pGr3R⇒Ves∝R
Surface area of Q=4A=4pR2Q
Surface area of P=A= 4pR2P ⇒RQ=2RP
Mass of R is MR=MP+MQ
r43pR3R=r43pR3P+r43pR3Q⇒R3R=R3P+R3Q=9R3P
RR=91/3RP⇒RR>RQ>RP ThereforeVR>VQ>VP,VRVP=91/3 and VPVQ=12
Topper's Solved these Questions
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive)ASSERTIOIN AND REASON
1 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive)MATCH MATRIX
1 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) SINGLE OPTION CORRECT
14 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )
111 Videos
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Advanced ( ARCHIVE LEVEL-2)
12 Videos
Similar Questions
Planet A has massa M and radius R. Planet B has half the mass and half the radius of Planet A.If the escape velocities from the Planets A and B are vAandvB, respectively , then vAvB=n4. The vlaue of n is :
View SolutionThe radius of a planet is double that of earth but their average are the same. If the escape velocities at the planet and the earth are vp and ve respectively , then prove that vp=2ve.
View SolutionTwo points P and Q are maintained at the potentials of 10V and -4V, respectively. The work done in moving 100 electrons from P to Q is:
View SolutionThree particales P,Q and R are placedd as per given Masses of P,Q and R are √3m√3m and m respectively The gravitational force on a fourth particle 'S' of mass m is equal to
 .
.
View SolutionTwo planets of masses M and M2 have radii R and R2 respectively. If ratio of escape velocities from their surfaces v1v2 is n4 , then find n :
View SolutionFind the relation between the gravitational field on the surface of two planets A and B of masses mA,mB and radii RA and RB,respectively if
a. they have equal mass.
b. they have equal (uniform)density.
View SolutionThe (m+n)thand(m−n)th terms of a G.P. are pandq respectively. Show that the mth and nth terms are √pqandp(qp)m/2n respectively.
View SolutionTwo concentric shells of uniform density of mass M1 and M2 are situated. The forces experienced by a particle of mass m when palced at positions A,B and C respectively are given OA =p,OB = q and OC =r .
 .
.
View SolutionA current I is passing through a wire having two sections P and O of uniform diameters d and d/2 respectively. If the mean drift velocity of electrons in section P and Q is denoted by vP and vQ respectively, then
View SolutionIf in the circuit shown below, the internal resistance of the battery is 1.5Ω and VP and VQ are the potential at P and Q respectively, what is the potential difference between the point P and Q?
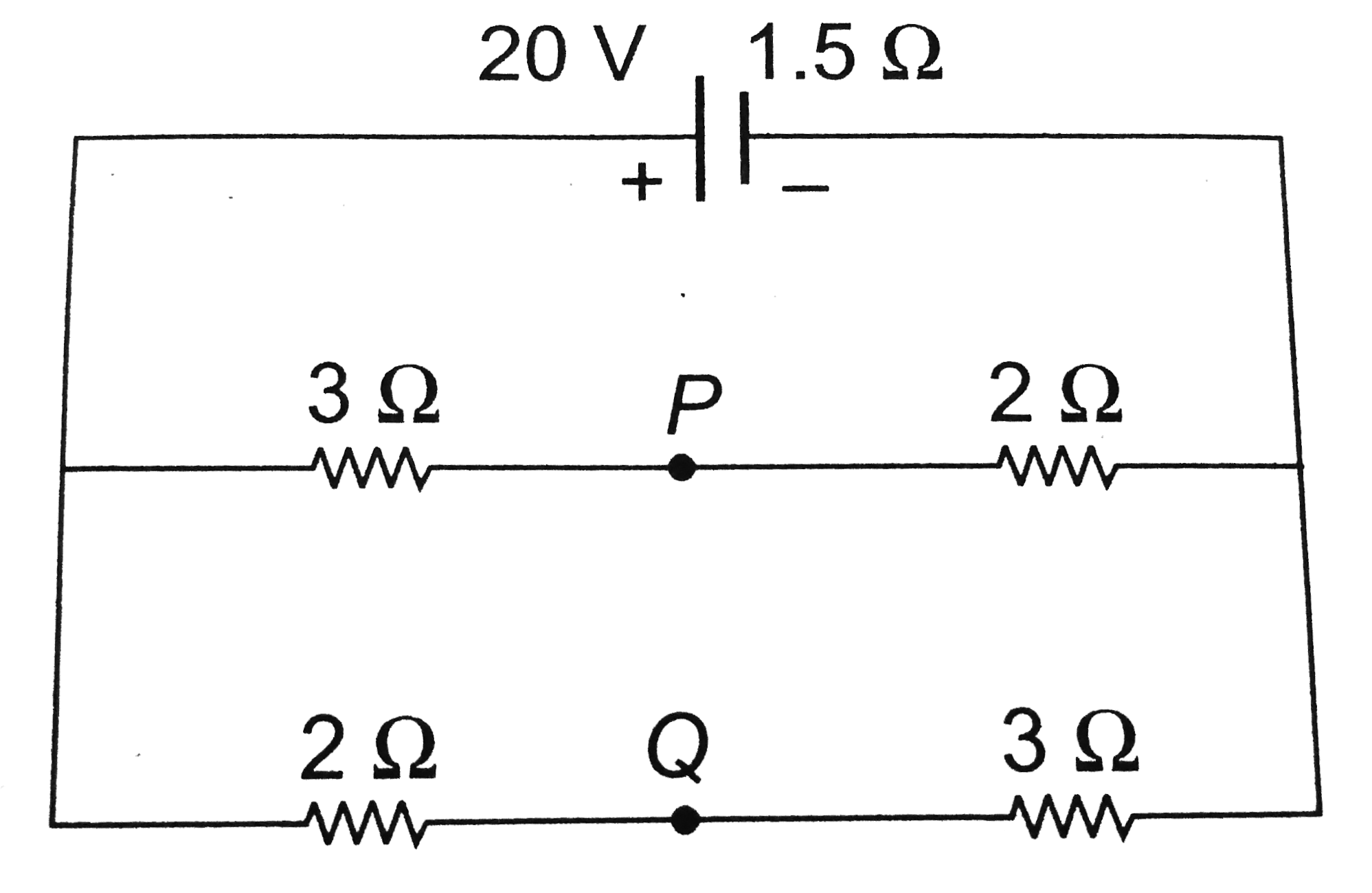
View Solution
