A(nonrotating) star collaps onto from an initial radius Ri with its mass remaining unchanged. Which curve in figure best gives the gravitational acceleration ag on the surface of the star as a function of the radius of the star during the collapse?
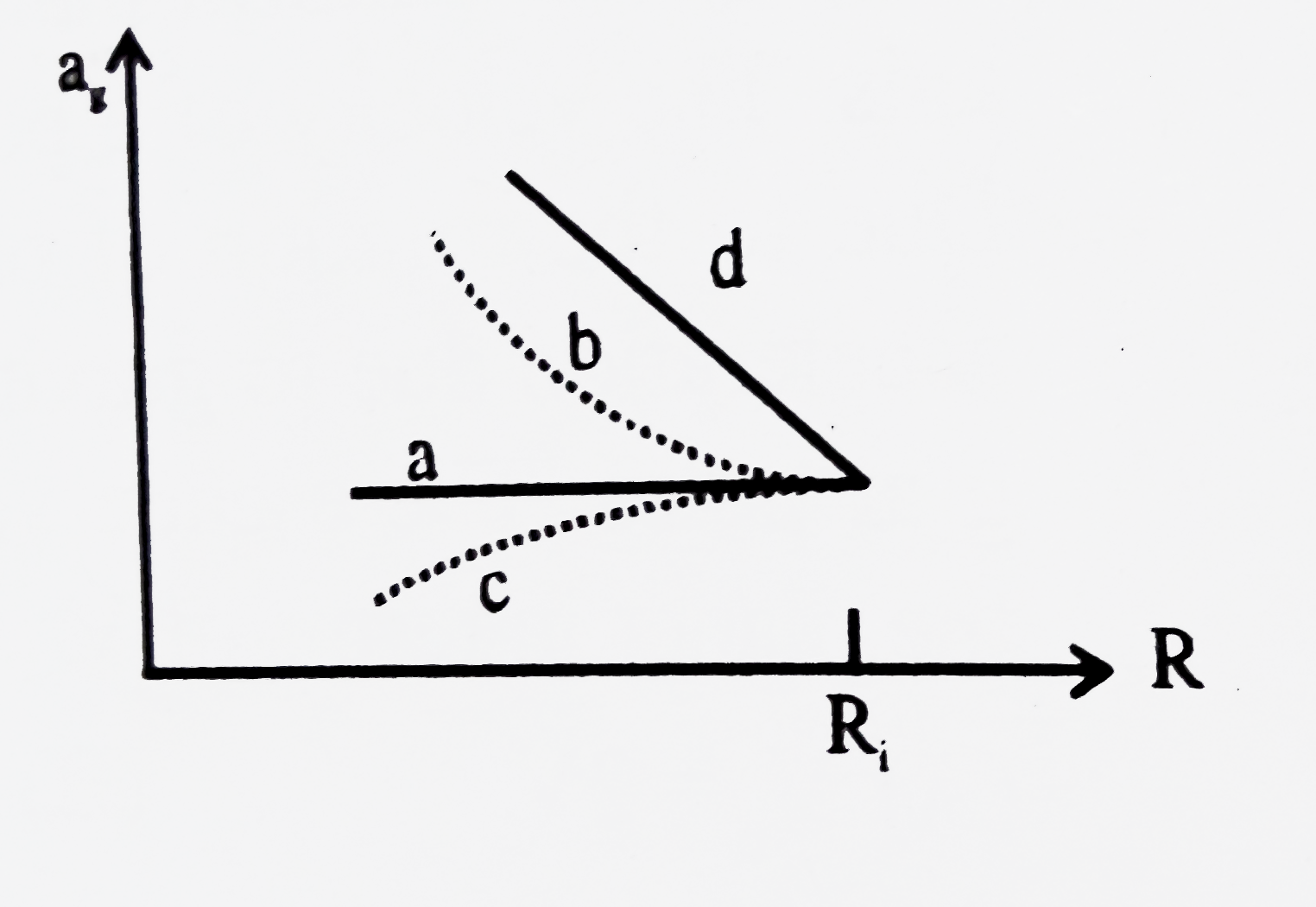
a
b
c
d
The correct Answer is:B
ag=GMr2

Topper's Solved these Questions
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Main (Archive)
43 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) SINGLE OPTION CORRECT
14 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level-1 MCQs
60 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )
111 Videos
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Advanced ( ARCHIVE LEVEL-2)
12 Videos
Similar Questions
A spherical hole of radius R/2 is excavated from the asteroid of mass M as shown in the figure the gravitational acceleration at a point on the surface of the asteroid just above the excavation is

View SolutionIf the mass of Mars is 0.107 ME and its radius is 0.53 RE, estimate the gravitational field g at the surface of Mars.
View Solution
Knowledge Check
If g be the acceleration due to gravity of the earth's surface, the gain is the potential energy of an object of mass m raised from the surface of the earth to a height equal to the radius R of the earth is
A(1/2) m g RB2 m g RCm g RD(1/4) m g R
A satellite of mass m revolves around the earth of radius R at a hight x from its surface. If g is the acceleration due to gravity on the surface of the earth, the orbital speed of the satellite is
View SolutionTwo stars of mass M1&M2 are in circular orbits around their centre of mass The star of mass M1 has an orbit of radius R1 the star of mass M2 has an orbit of radius R2 (assume that their centre of mass is not acceleration and distance between starts is fixed)
(a) Show that the ratio of orbital radii of the two stars equals the reciprocal of the ratio of their masses, that is R1/R2=M2/M1
(b) Explain why the two stars have the same orbital period and show that the period
T=2π(R1+R2)3/2√G(M1+M2) .
View SolutionAssuming the earth to be a homogeneous sphere of radius R, its density in terms of G (constant of gravitation) and g (acceleration due to gravity on the surface of the earth)
View SolutionThe gravitational potential energy of body of mass 'm' at the earth's surface -mgRe. Its gravitational potential energy at a height Re from the earth's surface will be (here Re is the radius of the earth)
View SolutionThe height from the surface of earth at which the gravitational potential energy of a ball of mass m is half of that at the centre of earth is (where R is the radius of earth)
View SolutionA small body of mass m falls to the earth from infintie distance away. What will be its velocity or reaching the earth? (Radius of the earth = R, acceleration due to gravity on the surface of the earth is g) :-
View SolutionIf the earth were to spin faster, acceleration due to gravity at the poles :
View Solution
