A body starts from rest from a point distant r0 from the centre of the earth. It reaches the surface of the earth whose radius is R. The velocity acquired by the body is
2GM(1R−1R0)
√2GM(1R−1R0)
GM(1R−1R0)
2GM√(1R−1R0)
The correct Answer is:B
To find the velocity acquired by a body that starts from rest at a distance r0 from the center of the Earth and reaches the surface of the Earth (radius R), we can use the principle of conservation of energy.
1. Identify Initial and Final States:
- The body starts from rest at a distance r0 from the center of the Earth. Therefore, its initial kinetic energy (KE) is 0.
- The potential energy (PE) at this point is given by:
PEi=−GMmr0
- When the body reaches the surface of the Earth (radius R), its potential energy is:
PEf=−GMmR
- At this point, it has acquired some kinetic energy, which we denote as KEf.
2. Apply Conservation of Energy:
- According to the conservation of mechanical energy:
PEi+KEi=PEf+KEf
- Since the body starts from rest, KEi=0:
−GMmr0+0=−GMmR+KEf
3. Rearranging the Equation:
- Rearranging the equation gives:
KEf=−GMmr0+GMmR
- This simplifies to:
KEf=GMm(1R−1r0)
4. Express Kinetic Energy in Terms of Velocity:
- The kinetic energy can also be expressed as:
KEf=12mv2
- Setting the two expressions for kinetic energy equal gives:
12mv2=GMm(1R−1r0)
5. Solving for Velocity:
- We can cancel m from both sides (assuming m≠0):
12v2=GM(1R−1r0)
- Multiplying both sides by 2 gives:
v2=2GM(1R−1r0)
- Finally, taking the square root to find v:
v=√2GM(1R−1r0)
Final Answer:
The velocity acquired by the body when it reaches the surface of the Earth is:
v=√2GM(1R−1r0)
- The body starts from rest at a distance r0 from the center of the Earth. Therefore, its initial kinetic energy (KE) is 0.
- The potential energy (PE) at this point is given by:
PEi=−GMmr0
- When the body reaches the surface of the Earth (radius R), its potential energy is:
PEf=−GMmR
- At this point, it has acquired some kinetic energy, which we denote as KEf.
- According to the conservation of mechanical energy:
PEi+KEi=PEf+KEf
- Since the body starts from rest, KEi=0:
−GMmr0+0=−GMmR+KEf
- Rearranging the equation gives:
KEf=−GMmr0+GMmR
- This simplifies to:
KEf=GMm(1R−1r0)
- The kinetic energy can also be expressed as:
KEf=12mv2
- Setting the two expressions for kinetic energy equal gives:
12mv2=GMm(1R−1r0)
- We can cancel m from both sides (assuming m≠0):
12v2=GM(1R−1r0)
- Multiplying both sides by 2 gives:
v2=2GM(1R−1r0)
- Finally, taking the square root to find v:
v=√2GM(1R−1r0)
The velocity acquired by the body when it reaches the surface of the Earth is:
v=√2GM(1R−1r0)
Topper's Solved these Questions
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Main (Archive)
43 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) SINGLE OPTION CORRECT
14 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level-1 MCQs
60 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )
111 Videos
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Advanced ( ARCHIVE LEVEL-2)
12 Videos
Similar Questions
A body is released from a point of distance R' from the centre of earth. Its velocity at the time of striking the earth will be (R’>Re)
View SolutionA body at rest starts from a point at a distance r (gtR) from the centre of the Earth. If M and R stand for the speed of the body when it reaches the Earth surface is
View Solution
Knowledge Check
The escape velocity from the surface of the earth is (where RE is the radius of the earth )
A√2gREB√gREC2√gRED√3gRE
The escape velocity of a body from the surface of the earth is equal to
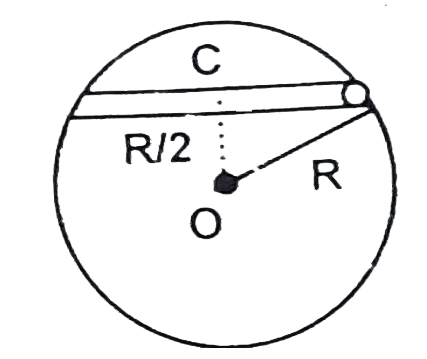
View SolutionA tunnel is dug across the earth of mass 'M' and radius 'R' at a distance R/2 from the centre 'O' of the Earth as shown. A body is released from rest from one end of the smooth tunnel. The velocity acquired by the body when it reaches the centre 'C' of the tunnel is
View SolutionA body projected from the surface of the earth attains a height equal to the radius of the earth. The velocity with which the body was projected is
View SolutionAn asteroid of mass m(m<<mE) is approaching with a velocity 12 km/s when it is at distance of 10 R from the centre of earth (where R is radius of earth). When it reaches at the surface of Earth, its velocity is (Nearest Integer) in km/s
View SolutionThe distance of geostationary satellite from the centre of the earth (radius R) is nearest to
View SolutionGravitational potential at a height R from the surface of the earth will be [Take M = mass of the earth, R = radius of the earth]
View SolutionA man weighs 'W' on the surface of the earth and his weight at a height 'R' from surface of the earth is (R is Radius of the earth )
View Solution
